Sottrazione di matrice

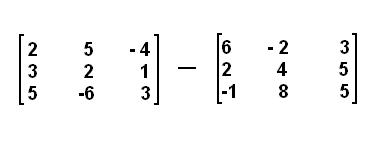
Per capire la nozione di sottrazione di matrice, dobbiamo prima sapere cosa sono le matrici in matematica. Una matrice è una serie di simboli e/o numeri che sono disposti in linee verticali e orizzontali e disposti come un rettangolo.

Ognuno dei numeri che compongono questa disposizione bidimensionale che chiamiamo matrice è chiamato voce, e deve essere disposto in righe (che sono anche note come righe) e colonne, come menzionato nel paragrafo precedente. Il modo di riferirsi a una matrice con n numero di righe e m numero di colonne è matrice n x m (si noti che la x è il segno di moltiplicazione, quindi si legge "per").

È importante notare che le matrici hanno varie applicazioni, alcune delle quali sono riassunte di seguito:

* in informatica: poiché sono caratterizzate dal fatto che permettono di manipolare l'informazione in modo facile e leggero (senza richiedere molta elaborazione), le matrici sono spesso usate per i calcoli numerici e per la rappresentazione di grafi (un insieme di vertici che sono collegati attraverso spigoli e sono usati per rappresentare relazioni di tipo binario tra vari elementi);

* teoria delle matrici: una branca della matematica che riguarda l'algebra, la statistica, la combinatoria e la teoria dei grafi;

* spazi vettoriali: strutture composte da vettori. In questo contesto, se si prendono due le cui dimensioni sono finite, una matrice può essere utilizzata per eseguire un'applicazione lineare tra di loro.

Con queste matrici, si possono eseguire diverse operazioni: tuttavia, alcune condizioni devono essere soddisfatte prima che le operazioni possano essere eseguite. Nel caso della sottrazione di matrici, è essenziale che le matrici in questione abbiano dimensioni identiche (devono avere lo stesso numero di colonne e righe).

Per sottrarre due matrici, quindi, è necessario sottrarre le componenti che si trovano nella stessa posizione l'una dall'altra. Prendiamo l'esempio di questa prima immagine, con le sue due matrici.

In questo caso, seguendo la definizione data sopra, dovremmo completare i seguenti passi per risolvere l'operazione. Cominciamo con la prima colonna (cioè con i numeri in verticale):

2 - 6 = - 4
3 - 2 = 1
5 - (-1) = 6

Poi continuiamo con la seconda colonna:

5 - (-2) = 7
2 - 4 = - 2
- 6 - 8 = - 14

Infine, sottraiamo gli elementi della terza colonna:

- 4 - 3 = - 7
1 - 5 = - 4
3 - 5 = - 2

Quindi, dobbiamo solo ordinare i numeri per ottenere il risultato di questa sottrazione di matrici, come si può vedere in questa seconda immagine.

La sottrazione di matrici, in breve, consiste nel sottrarre i diversi componenti di ogni matrice, sempre rispettando il posto che occupano nella struttura. Se le matrici hanno un numero diverso di componenti, l'operazione non può essere completata. Vale la pena ricordare che lo stesso vale per l'addizione (o aggiunta) di matrici. Tuttavia, non c'è alcuna restrizione sul rapporto tra il numero di righe e il numero di colonne.

Una matrice che ha lo stesso numero di colonne come righe è conosciuta come una matrice quadrata perché sembra un quadrato quando viene tracciata. Come menzionato nel paragrafo precedente, è perfettamente possibile sottrarre (e aggiungere) due matrici le cui forme non sono quadrate: l'importante è che per ogni coppia ci sia una coppia corrispondente.

È essenziale capire che questo concetto e molti altri della matematica possono essere usati nella vita quotidiana, e che non sono argomenti per pochi abili. La maggior parte delle persone probabilmente lavora con le matrici più spesso di quanto si renda conto, anche se non le riconosce come tali; dopo tutto, sono una tecnica per mettere in relazione e organizzare i dati. La sottrazione di matrici, così come altre operazioni, è anche spesso applicata se in due liste di elementi corrispondenti tra loro abbiamo bisogno di sapere quanto rimane della prima una volta che sono influenzate dalla seconda.