Sottrazione di polinomi

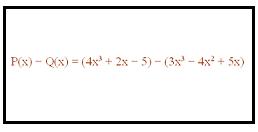
Un polinomio è un'espressione algebrica formata dall'unione di due o più costi variabili, ottenuti con operazioni di sottrazione, addizione o moltiplicazione. Con i polinomi si possono eseguire diversi calcoli.

Per eseguire un file di sottrazione di polinomi, è necessario raggruppare i file dei monomi (le espressioni singole) secondo le loro caratteristiche e procedere alla semplificazione di quelli simili. La stessa operazione si fa aggiungendo il contrario del sottraendo al minuendo.

Prendiamo il seguente esempio: P (x) - Q (x) = (4 × 3 + 2x - 5) - (3 × 3 - 4 × 2 + 5x)

Come spiegato sopra, dobbiamo modificare il file segni del sottraendo per eseguire l'operazione: 4 × 3 + 2x - 5 - 3 × 3 + 4 × 2 - 5x. Come puoi vedere, i segni del minuendo non cambiano (4 × 3 + 2x - 5).

Fatto ciò, dobbiamo raguppare e semplificare i monomi: 4 × 3 - 3 × 3 × 3 + 4 × 2 + 2x - 5x - 5.

Infine completiamo l'operazione secondo i monomi rimasti: x3 + 4 x 2 - 3x - 5.

Il risultato della sottrazione dei polinomi (4 × 3 + 2x - 5) - (3 × 3 - 4 × 2 + 5x) è, in breve, x3 + 4 x 2 - 3x - 5.

Un altro modo di sottrarre i polinomi è scrivere l'opposto dell'altro. Pertanto, monomi simili diventeranno colonnari e possiamo procedere alla loro addizione.

È importante notare che non importa quale delle tecniche di sottrazione di polinomi scegliamo: il risultato dell'operazione, se eseguita correttamente, sarà lo stesso.

I polinomi hanno varie applicazioni al di fuori del regno della matematica e, come per molti altri concetti a prima vista troppo specifici, non sempre ne siamo consapevoli. Una delle aree in cui sono di grande aiuto è l'allineamento delle antenne elettromagnetiche, qualcosa che molte persone fanno ogni giorno quando installano reti Internet senza fili (Wi-Fi).

Per progettare un'antenna a 2,4 GHz in grado di collegare dispositivi a una rete Wi-Fi, è necessario utilizzare il Polinomi Chebyshev, che permette di distribuire correttamente la corrente in ogni elemento dell'array e trova le dimensioni fisiche appropriate in base a questi dati. I polinomi di Chebyshev prendono il nome dal matematico russo Pafnuti Chebyshev, e sono una famiglia che può essere facilmente definita in modo lineare, la stessa dei numeri di Fibonacci, per esempio.

Un'ulteriore applicazione dei polinomi è in biologia, poiché è possibile calcolare la popolazione di una batteria per mezzo di espansioni polinomiali. Con l'espansione di un prodotto di coppie si intende in matematica una coppia di prodotti (la moltiplicazione è distributiva rispetto alla coppia); nel caso dei polinomi, questa può essere ottenuta sostituendo ripetutamente le sottoespressioni che moltiplicano altre due (almeno una delle quali deve essere una coppia) con la coppia di prodotti equivalente, e così via fino a quando l'intera espressione diventa una coppia di prodotti.

In biologia, i polinomi sono usati per calcolare la struttura tridimensionale delle proteine (cristallografia a raggi X) e per determinare quanto una malattia si diffonde per contatto tra un gruppo di neonati e un gruppo di persone sane. Le statistiche sono anche utili, anche più di altri campi; per esempio, per stimare le vendite potenziali di un'azienda nel prossimo anno finanziario o per prevedere il tempo tenendo conto di variabili come temperatura, massa d'aria e pressione.

Come si può vedere, la sottrazione dei polinomi è un processo semplice rispetto ad altre che coinvolgono anche questo tipo di espressioni algebriche, ma ciò non significa che non sia presente come parte di alcune di esse.