Sottrazione vettoriale

Il vettore è una nozione che ha diversi usi. Può essere l'agente responsabile dello spostamento di una cosa da un luogo a un altro; una proiezione con intensità e caratteristiche variabili; una grandezza che ha un punto di applicazione, una direzione e un verso; o l'organismo capace di trasmettere certe malattie.

Cioè, un vettore è uno strumento che dà la possibilità di intraprendere la rappresentazione di grandezze vettoriali, che non solo hanno bisogno di un senso ma anche di una direzione e di una quantità specifica.

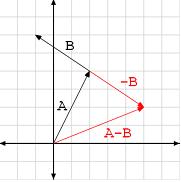
La nozione di sottrazione di vettori è usata in matematica. In questo caso, il vettore è una quantità che viene rappresentata graficamente come un segmento che ha origine in un punto A ed è orientato verso la sua estremità (punto B). Il vettore, quindi, è un segmento AB.

La sottrazione vettoriale è un'operazione eseguita su due segmenti di questo tipo. Per eseguire la sottrazione di due vettori, ciò che si fa è prendere un vettore e aggiungere il suo opposto ad esso.

Supponiamo di voler eseguire la seguente sottrazione: AB - DE, essendo AB (-3, 4) e DE (5, -2) secondo la posizione dei vettori nel piano cartesiano. Tenendo presente quanto detto sull'addizione dell'opposto, dovremmo porre l'operazione in questo modo:

(-3, 4) - (5, -2)
(-3-5, 4+2)
(-8, 6)


Come si vede, a -3 si aggiunge l'opposto di 5 (cioè -5), mentre a 4 si aggiunge l'opposto di -2 (cioè 2). Così, il risultato di questa sottrazione di vettori è (-8, 6).

Se, invece, avessimo aggiunto i vettori, l'operazione era più semplice poiché bastava aggiungere le componenti:

(-3, 4) + (5, -2)
(-3 + 5, 4-2)
(2, 2)

Si considera che aggiungere vettori è molto meno complesso che sottrarli. Per realizzare la prima operazione, tutto quello che dovete fare è mettere l'inizio della seconda dopo la fine della prima, l'inizio della terza dopo la fine della seconda e così via, fino ad utilizzare tutti i vettori con cui volete operare.

Altri aspetti importanti da tenere a mente sui vettori e le operazioni che si possono realizzare con essi sono i seguenti:
-Aggiungere, sottrarre e moltiplicare sono le operazioni che si possono realizzare con essi.
-Quando si sommano o si sottraggono vettori, ciò che si ottiene è ottenere un altro vettore e questo può essere ottenuto attraverso diversi tipi di procedure, numeriche o geometriche.
-La sottrazione può essere effettuata attraverso le coordinate cartesiane date dei vettori, sia nello spazio che in quello che sarebbe il piano.
-Aggiunte e sottrazioni di vettori nello spazio possono essere combinate.
- Il contrario di qualsiasi vettore ha sempre la stessa misura di questo ma è in una direzione opposta.