Funzione logaritmica

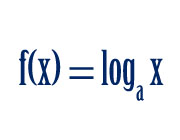
Il concetto di funzione ha molteplici usi. Se ci concentriamo sulla matematica, una funzione è una relazione che esiste tra due insiemi, per cui ad ogni elemento dell'insieme iniziale viene assegnato un solo elemento dell'insieme finale (o nessuno). Logaritmico, invece, è ciò che è legato a un logaritmo: l'esponente a cui bisogna elevare una certa quantità per ottenere un certo numero come risultato.

Da queste idee, possiamo passare alla definizione di una funzione logaritmica. Questa è la funzione la cui espressione generica si vede nell'immagine.

In queste funzioni, a è la base, che deve essere positiva e diversa da 1. Il modo ufficiale di leggere questa equazione è il seguente: "la funzione di x è uguale al logaritmo base a di x". Vale la pena ricordare che potrebbe anche essere espresso senza l'uso dell'espressione f(x), ma con una variabile come y, poiché in questo modo potremmo riflettere più chiaramente che il risultato è un elemento diverso, da un altro insieme.

È importante ricordare che la funzione logaritmica è la funzione inversa della funzione esponenziale: quella che è rappresentata dall'equazione f(x) = aˣ

Tra le caratteristiche principali di una funzione logaritmica, possiamo menzionare che il suo dominio (il suo insieme iniziale) sono i numeri reali positivi. È una funzione continua, il cui percorso è R (le immagini ottenute applicando la funzione corrispondono a uno qualsiasi degli elementi dell'insieme formato dai numeri reali).

Un'altra proprietà è che la funzione logaritmica della base è uguale a 1 in tutti i casi. Le funzioni logaritmiche, invece, possono essere crescenti o decrescenti, così come convesse o concave, a seconda del valore della base. Per sapere se sono crescenti, basta osservare se a è maggiore di 1; d'altra parte, se è maggiore di 0 e minore di 1, allora è decrescente.

Continuando con le proprietà della funzione logaritmica, possiamo dire che nel grafico troviamo sempre i seguenti due punti: (1, 0) e (a, 1), intendendo questi duplicati come valori sugli assi X e Y, cioè gli assi orizzontale e verticale, rispettivamente. Anche la funzione logaritmica è considerata iniettiva.

Nel campo della matematica, una funzione iniettiva è quella in cui ogni elemento del codominio corrisponde a un solo elemento del dominio. In altre parole, in una funzione di questo tipo, alla quale appartiene anche la funzione logaritmica, non può essere il caso che più di un elemento del primo insieme abbia la stessa immagine.

Quando si graficizza una funzione logaritmica si ottiene un risultato simmetrico a quello della funzione esponenziale se si tiene conto della bisettrice del primo e del terzo quadrante. Per bisettrice si intende la semiretta che parte dal vertice di un angolo e lo taglia in due parti identiche. La ragione di questo fenomeno è che entrambi sono inversi o reciproci l'uno dell'altro.

Le funzioni logaritmiche, in breve, sono quelle nella cui equazione la variabile è la base o argomento di un logaritmo. Per risolvere queste equazioni, di solito si tratta di convertire l'equazione logaritmica in una equivalente ma senza logaritmo.

Nei casi che possono essere rappresentati dall'equazione nella prima immagine, la conversione imposta la base del logaritmo come quella di una potenza elevata alla x ed eguaglia questo termine alla y. Per esempio, se abbiamo una funzione di x in cui la base è 2, per ogni elemento del codominio dobbiamo trovare quale numero è uguale ad esso se lo squadriamo.