Vettori concorrenti

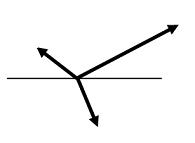
Vettore è un concetto con diversi usi. In questo caso, ci interessa il suo significato nel campo della fisica, che indica che un vettore è una grandezza definita dal suo valore, il suo senso, la sua direzione e il suo punto di applicazione. Concorrente, invece, è ciò che concorre (cioè che si unisce o coincide con qualcos'altro).

I vettori possono essere classificati in diversi modi secondo le loro caratteristiche. I vettori che passano per lo stesso punto sono chiamati vettori concomitanti. Dato che, passando per un tale punto, creano un angolo, i vettori concorrenti sono anche chiamati vettori angolari.

Supponiamo che due elicotteri decollino dallo stesso punto. Uno degli aerei è diretto a est e l'altro a ovest. Entrambi gli elicotteri prendono un percorso che può essere rappresentato da un vettore; poiché hanno lo stesso punto di applicazione, sono vettori concorrenti.

Prendiamo il caso di un architetto che disegna la finestra di una stanza. Nel piano, per rappresentare la finestra, fa un rettangolo con quattro vettori: A, B, C e D. Secondo quanto detto sopra, possiamo dire che A e B, B e C, C e D, e D e A sono vettori concorrenti, poiché si intersecano. D'altra parte, A e C non sono vettori concomitanti, né lo sono B e D.

Uno degli aspetti che rende i vettori così particolari nel campo della fisica è che non rappresentano solo un valore isolato, ma combinano una lunghezza con un orientamento, ed è grazie a questo che sono strumenti così versatili, con così tante applicazioni in diversi campi.

Come si può dedurre dai paragrafi precedenti, i vettori possono essere utilizzati sia in spazi bidimensionali che tridimensionali, ed è in questi ultimi che li troviamo più spesso: gli esempi precedenti mostrano un caso in tre dimensioni (gli elicotteri) e un altro in due (la finestra).

Facendo uso della suddetta versatilità dei vettori e dei loro numerosi campi di applicazione, pensiamo a un esempio che completi i due precedenti. In questo caso, non rappresenteranno il movimento di un veicolo o una serie di segmenti disegnati per dare un disegno adeguato: saranno due o più corde che tirano un oggetto, dallo stesso punto.

Se leghiamo una corda intorno a una scatola pesante e lasciamo che le sue due estremità emergano dal nodo, possiamo condividere il suo peso con un'altra persona, poiché ognuno può tirare una di esse. In questo caso, i vettori concorrenti dimostrano chiaramente il concetto di addizione vettoriale, poiché nonostante l'esistenza di due orientamenti e forze diverse, la scatola si muoverà in una sola direzione.

Nella seconda immagine si può vedere che dallo stesso punto di partenza dei due vettori concorrenti disegnati in rosso ne emerge un terzo, concorrente ad entrambi, che indica la direzione in cui l'oggetto legato con la corda e tirato da due persone si muoverà.

La formula per calcolare il valore di questo nuovo vettore si trova anche nell'immagine: basta sommare le componenti corrispondenti.

Per rappresentare graficamente la somma, è possibile utilizzare il metodo del parallelogramma: consiste nel disegnare due linee rette, ciascuna parallela a uno dei vettori e passante per l'estremità dell'altro, in modo che quando si intersecano si intersechino in un punto che serve a chiudere la figura. Questo punto sarà la fine del nuovo vettore.

Oltre ai vettori concorrenti, altre classi di vettori sono vettori unitari, vettori collineari, vettori complanari, vettori paralleli e vettori opposti.