Triangolo ottuso

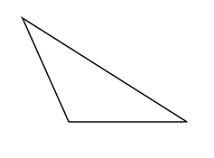
Sul terreno della geometria, si chiamano figure piane delimitate da un certo numero di segmenti poligonali. Se il poligono è composto da tre segmenti (chiamati lati), la figura è un triangolo.

In base alle sue caratteristiche specifiche, un triangolo può essere classificato in diversi modi. Il triangolo ottone è quello che ha un angolo ottone: cioè, misura più di 90°. Dei tre angoli interni del triangolo ottone, quindi, uno è ottone, mentre gli altri due sono appuntiti (meno di 90°).

Tutti i triangoli ottone sono triangoli ottone perché nessuno dei loro angoli interni è appuntito. I triangoli acuti, che hanno tre angoli acuti, immettono questa stessa valutazione. Se il triangolo ha un angolo arrotondato, invece, è classificato come un triangolo rotondo (e non è ottone, acuto o obliquo).

È importante notare che i triangoli ottone possono anche essere inclusi in altri insiemi a seconda delle caratteristiche dei loro lati. Il triangolo ottone che ha due lati che mostrano la stessa cosa e un terzo lato diverso è un triangolo isoscele. Se il triangolo ottone ha tre lati diversi, tutti con dimensioni diverse, è un triangolo scaleno.

Come si può notare, uno stesso triangolo può essere classificato in più di un modo, a seconda del criterio concentrato sui suoi angoli o sui suoi lati. Un triangolo, in questo modo, può essere anche isoscele o scaleno così come ovoidale e obliquo, perché le prime due classificazioni dipendono dai lati e le altre due dagli angoli.

I triangoli sono figure apparentemente molto semplici, le meno complesse di tutte se vogliamo, ma nascondono un gran numero di concetti e applicazioni che sono più che utili per risolvere una miriade di problemi matematici e fisici. In primo luogo, non dobbiamo pensare al triangolo come a un corpo che funziona solo se conosciamo tutti i lati e gli angoli: molte volte, è pensando in questo modo e utilizzando alcune delle numerose equazioni ad esso associate che possiamo trovare una soluzione a un problema che sembra avere poca correlazione con la geometria.

Detto questo, consideriamo che per trovare un triangolo ci sono almeno due modi, uno per ogni estremità: disegnarlo; dedurre la sua presenza attraverso le equazioni che relazionano i suoi lati ai suoi angoli. Il primo caso non è strettamente vincolante, o almeno non per la scienza: prendiamo un piccolo pezzo di legno, tracciamo tre linee collegate tra loro e, voilà. D'altra parte, rendersi conto di essere di fronte di un triangolo quando la sua esistenza non è evidente può far uscire da più di un vicolo cieco.

Consideriamo una situazione in cui occorre conoscere la posizione relativa che avrebbe un punto se passasse da un piano all'altro, parallelamente al primo; più speciamente, la posizione che avrebbe un oggetto nell'universo tridimensionale si se spostasse in quello bidimensionale da cui viene osservato. Questo può essere necessario quando si sviluppa un videogioco in cui è necessario utilizzare una grafica bidimensionale come aspetto, sempre sullo schermo, e farla riaggregare ogni volta che passa "sopra" certi oggetti tridimensionali, perché lo schermo si misura in pixel.., mentre l'universo 3d usa unità arbitrarie.

Bene, poiché la telecamera che cattura la scena ha un determinato campo visivo (un angolo verticale e un angolo orizzontale, che formano una piramide immaginaria, al di fuori della quale non viene mostrato alcun oggetto), possiamo usare questi angoli insieme alla distanza tra la telecamera e ogni oggetto tridimensionale (che faremo più grande di un triangolo) per risolvere il problema. Prima di continuare, dobbiamo capire che questi campi visivi disegnano due triangoli di classi diverse (se un angolo è maggiore di 90°, saremo di fronte a un triangolo ottuso), ma tagliandoli in due, otterremo quattro linee rette.

Fatto ciò, dobbiamo semplicemente applicare le equazioni pertinenti per scoprire la gamba rimanente (una volta per il file angolo verticale e un'altra per l'orizzontale, che ora misurano la metà), e duplicarle per conoscere le dimensioni dello spazio in cui si trova l'oggetto; infine, trasferiamo la sua posizione sullo schermo mettendo in relazione queste dimensioni con la risoluzione in pixel.