Frazione equivalente - Che cos'è, significato e concetto

Nel campo della matematica, un'espressione che si riferisce alla divisione è chiamata frazione. La frazione 1/3, per esempio, implica che il numero 1 è diviso per 3 (o, in altre parole, 1 diviso per 3). Due o più elementi equivalenti, allo stesso tempo, sono simili o pari.

Per costruire una frazione matematica, dobbiamo avere due componenti: Un numeratore e un denominatore. Nel paragrafo precedente viene citato l'esempio 1 / 3, che dovremmo leggere "un terzo"; in questo caso abbiamo un numeratore di valore 1 e un denominatore che è 3. Il significato di tale copia è che siamo di fronte a un terzo di un intero, una quantità che per raggiungere l'altro deve essere moltiplicata per tre.

Va da sé che numeratori e denominatori devono essere sempre interi minori di zero, cioè gli elementi dell'insieme che ha i numeri naturali da meno di infinito a più di infinito. Senza entrare in questioni troppo tecniche, è sufficiente comprendere il concetto di frazione per capire questa regola: poiché essa esprime un rapporto in sé, e il processo di dividere il suo numeratore per il suo denominatore più di una volta ci dà un risultato con un segno, non sarebbe logico costruirla con i numeri decimali.

Per leggere una frazione è necessario conoscere un tipo speciale di parola: il numerale. Quando scriviamo un numero abbiamo due opzioni: usare i numeri appropriati in base al sistema usato o scrivere i loro nomi in parole, e per questo abbiamo i numerali.

I numerali sono nomi propri per designare i numeri; in altre parole, sono parentesi che servono per riferirsi ad essi attraverso la lingua scritta o parlata. Ci sono diversi tipi di numeri e l'uso dell'uno o dell'altro dipende dal concetto matematico che vogliamo esprimere a parole. Per esempio, i numeri cardinali (detti anche numeri comuni) sono quelli che usiamo ogni giorno per riferirci ai numeri quando dobbiamo contare degli oggetti: uno, due, tre e così via.

Nel caso delle frazioni, equivalenti o meno, i numeri cardinali si usano per riferirsi al loro numeratore. Dall'altra parte, ci sono i numeri frazionari, conosciuti anche come numeri partitivi, che si usano per esprimere la divisione di un intero in più parti: metà, terzo, quarto e così via. Il denominatore di una frazione si scrive usando questi termini.

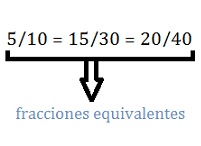
Le frazioni equivalentiIn questo modo sono quelle che, sebbene scritte diversamente, rappresentano la stessa quantità. 5 / 10, 15 / 30 e 20 / 40Per citare alcuni esempi, queste sono frazioni equivalenti. Vediamo un controllo che si ottiene dividendo i loro numeratori per i loro denominatori:

5 / 10 = 0,5
15 / 30 = 0,5
20 / 40 = 0,5

Si può affermare che queste frazioni (5 / 10, 15 / 30 e 20 / 40) sono frazioni equivalenti poiché tutte e tre indicano la stessa quantità: 0,5.

Un modo semplice per scoprire se due o più frazioni sono equivalenti è moltiplicare il numeratore e il denominatore di ciascuna per lo stesso numero. Questo processo è noto come amplificazione.

Tornando all'esempio precedente, possiamo provare con il numero 3:

(5 x 3) / (10 x 3) = 15/30 = 0,5
(15 x 3) / (30 x 3) = 45/90 = 0,5
(20 x 3) / (40 x 3) = 60/120 = 0,5

La semplificazione è un processo simile, basato sulla divisione del numeratore e denominatore per lo stesso numero. È importante notare che per completare questa operazione i due termini devono essere divisibili per il numero in questione. Se il risultato è lo stesso, allora dobbiamo farlo con frazioni equivalenti. Possiamo fare la prova con gli esempi precedenti e il numero 5:

(5/5) / (10/5) = 1/2 = 0,5
(15/5) / (30/5) = 3/6 = 0,5
(20/5) / (40/5) = 4/8 = 0,5

L'utilità delle frazioni equivalenti sta nella possibilità di trovare una versione più piccola di un'altra, che rende meno complicato un certo calcolo, per esempio. D'altra parte, riconoscendo due o più frazioni equivalenti in un'operazione, la si può semplificare permettendo di rimuoverle o associarle.