Angoli adiacenti

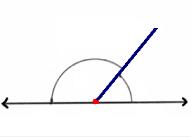
Un angolo è una figura geometrica formata da due linee rette che condividono lo stesso vertice dell'origine. Adiacente, invece, è un aggettivo che qualifica ciò che si trova accanto a qualcosa.

Gli angoli adiacenti sono quelli che condividono un lato e il vertice, mentre gli altri due lati risultano di raggio opposto. Questa definizione ci permette di dedurre che gli angoli adiacenti sono anche angoli contigui o consecutivi (perché hanno un lato in comune e lo stesso vertice) e angoli supplementari (la somma dei due risulta in 180°; cioè, un angolo retto).

È importante notare che non tutte le fonti su questo argomento rispettano il requisito che entrambi gli angoli sommino a un totale di 180°; cioè, molti testi di geometria definiscono il concetto di angoli adiacenti come qualsiasi coppia che abbia un lato e un vertice in comune, senza bisogno che siano supplementari. Per questo motivo, prima di consultare informazioni sull'argomento, è necessario identificare la convenzione a cui risponde, per evitare contraddizioni o mancanza di coerenza.

Altra proprietà degli angoli adiacenti è che i loro coseni hanno lo stesso valore, sebbene di segno inverso, cioè che il loro valore assoluto è lo stesso; per esempio, se prendiamo due angoli adiacenti, uno di 120° e l'altro di 60°, il coseno del primo è uguale al coseno del secondo moltiplicato per -1. I seni di questi angoli, invece, sono uguali.

Il coseno è un concetto che appartiene alla trigonometria, e si riferisce al rapporto tra la gamba adiacente di un angolo acuto che fa parte di un triangolo rettangolo e la sua ipotenusa; in altre parole, possiamo dire che il coseno dell'angolo α è uguale alla divisione della sua gamba adiacente per il valore dell'ipotenusa. Va notato che il risultato non varia a seconda delle caratteristiche del triangolo rettangolo, ma è una funzione dell'angolo, come indicato dal Teorema di Talete.

D'altra parte, c'è il seno, una funzione trigonometrica che consiste nel dividere la gamba opposta di un dato angolo per la sua ipotenusa.

Se un angolo di 44° si trova accanto a un angolo di 136°, con cui condivide un lato e il vertice, possiamo dire che sono angoli adiacenti (44° + 136° = 180°). Questa qualificazione riguarda entrambi gli angoli, senza impedire lo sviluppo di altre classificazioni. L'angolo di 44°, oltre ad essere adiacente all'altro, è un angolo acuto. L'angolo di 136°, d'altra parte, è adiacente a questo angolo acuto, ma è esso stesso un angolo ottuso.

Due angoli retti (di 90° ciascuno) possono anche essere angoli adiacenti. Il requisito è sempre lo stesso: devono condividere un vertice e un lato, e gli altri due lati devono essere angoli semidestri opposti. Se sommiamo entrambi gli angoli retti adiacenti, il risultato sarà un angolo retto (180°).

Come per molte altre classificazioni in matematica, il concetto di angoli adiacenti può essere applicato a molti problemi diversi. Una volta che abbiamo identificato il tipo di angolo con cui abbiamo a che fare, il passo successivo è quello di andare a una fonte affidabile per studiare tutte le sue proprietà conosciute, e valutare la sua utilità per il nostro progetto.

Si può dire che non sempre i due angoli necessari per dare vita a questo concetto sono espressamente presenti, ma spesso si parte da uno e si immagina l'altro per accedere a queste proprietà, se questo apre la porta a nuove soluzioni. In altre parole, non dobbiamo dimenticare che si tratta di concetti che nascono dall'osservazione e dalla teorizzazione e che ci permettono di plasmare la realtà alle nostre esigenze.