Proposizione matematica

La proposizione è un concetto con diversi usi. Può essere la manifestazione di qualcosa in modo che altri individui conoscano un'intenzione, la concretezza di una proposizione, o un'affermazione che può essere falsa o vera.

La matematica, d'altra parte, è la scienza dedicata all'analisi di entità astratte, come numeri, figure geometriche e simboli, e le loro proprietà. Come aggettivo, il termine si riferisce a tutto ciò che è legato a questa disciplina deduttiva.

Dopo queste precisazioni, possiamo concentrarci sulle proposizioni matematiche. Una proposizione matematica è un'espressione algebrica che può portare due valori: essere vera o essere falsa, anche se mai entrambi allo stesso tempo.

Denominate con lettere minuscole, le proposizioni matematiche hanno un valore di verità (che sarà la verità o la falsità della loro dichiarazione). Secondo le loro caratteristiche, è possibile distinguere tra proposizioni semplici (che mancano di connettori logici) e proposizioni composte (che hanno più di un connettore logico). All'interno di questi gruppi si possono notare anche altre classificazioni: proposizioni relazionali, proposizioni predicative, ecc.

Le proposizioni matematiche possono essere viste come espressioni di giudizio che non possono essere vere e false contemporaneamente. Per esempio:

a: 9 è un multiplo di 3

Tale espressione è una proposizione matematica che è vera, poiché 3 x 3 è uguale a 9 e, quindi, 9 è uno degli infiniti multipli di 3. Come abbiamo detto sopra, la proposizione matematica può anche essere falsa:

b: 7 è un multiplo di 3

In questo caso, la proposizione è falsa perché 7 non è tra i multipli di 3 (3 x 2 = 6, 3 x 3 = 9).

Proposizione matematica aperta

Ci sono certe affermazioni di cui non possiamo anticipare il valore di verità a prima vista, poiché nel loro contenuto c'è almeno una variabile, il cui valore è sconosciuto. Dopo averla osservata e analizzata, si possono fare i calcoli necessari per trovare uno dei valori in grado di sostituirla, per poter finalmente essere sicuri se la proposizione è vera o falsa.

In alcuni casi, le variabili possono essere sostituite da più di un valore, che fanno parte di un insieme chiamato dominio della variabile. A sua volta, l'insieme formato dagli elementi di quel dominio che rendono vera la proposizione aperta si chiama l'insieme delle soluzioni della proposizione aperta.

Proposizione matematica congiuntiva

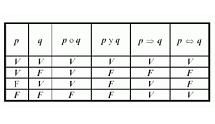
Quando due proposizioni sono unite per mezzo del simbolo di congiunzione (^), si parla di una proposizione congiuntiva, che deve soddisfare la seguente condizione: essa può avere un valore di verità vero solo se anche i suoi due componenti sono veri; d'altra parte, se almeno uno di essi dà il valore falso, allora la proposizione congiuntiva è falsa.

Siccome stiamo trattando la relazione tra due insiemi, è anche possibile determinare quegli elementi che fanno parte di entrambi i domini variabili, che appartengono all'insieme di intersezione di entrambe le proposizioni matematiche.

Proposizione matematica disgiuntiva

In questo caso, anche due proposizioni sono collegate, ma si usa il simbolo opposto al precedente, che può essere letto come la parola "o", dato che propone una relazione caratterizzata dal seguente requisito: la proposizione disgiuntiva può avere un valore vero solo se le sue due componenti sono false, mentre è sufficiente che una di esse sia vera perché sia vera anche la prima.

Implicazione

Questo tipo di proposizione matematica si chiama anche condizionale e consiste in una connessione che ha luogo se si compie quanto segue: è falsa solo quando la prima proposizione (detta antecedente) è vera e la seconda (la conseguente) è falsa; qualsiasi altro caso darà come risultato un valore vero.