Funzione iniettiva

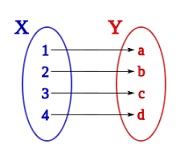
Nel contesto della matematica, una funzione è il legame che si sviluppa tra due insiemi, per cui ad ogni elemento di un insieme viene assegnato un singolo elemento di un altro insieme o nessuno. L'idea di iniettivo o iniettiva, invece, allude alla proprietà che a due elementi diversi di un primo insieme corrispondono due elementi diversi di un secondo insieme.

Una funzione iniettiva, quindi, è quella che, a elementi diversi dell'insieme iniziale (il dominio), corrispondono elementi diversi dell'insieme finale (il codominio). Questo significa che ogni elemento del codominio non ha più di una preimmagine nel dominio: o, espresso in un altro modo, che ogni elemento del dominio non può avere più di un'immagine nel codominio.

L'espressione per una funzione iniettiva è f : x -> y. Prendiamo il caso di un insieme X composto da Argentina, Svizzera e Nigeria, e un insieme Y composto da America, Europa e Africa. Se volessimo stabilire una relazione tra ogni paese e il suo continente corrispondente, otterremmo una funzione iniettiva, poiché i legami sarebbero i seguenti:

Argentina -> America
Svizzera -> Europa
Nigeria -> Africa

Con gli insiemi menzionati e la relazione indicata, gli elementi del primo insieme (i paesi) non potrebbero mai corrispondere a più di una immagine nel secondo insieme (i continenti). L'Argentina appartiene all'America e non all'Europa o all'Africa. La Svizzera, invece, è solo in Europa (non in America o in Africa). La Nigeria, infine, fa solo parte dell'Africa, senza essere in America o in Europa. In questo caso, insomma, entrambi gli insiemi sono collegati da una funzione iniettiva.

Guardiamo ora un esempio in cui i requisiti perché la funzione sia considerata iniettiva non sono soddisfatti. È il caso della funzione che ammette tutti i numeri reali ed è definita come f(x) = x.x: poiché è possibile utilizzare sia numeri negativi che positivi per sostituire la variabile x, ogni risultato (che per convenzione è rappresentato dalla variabile y) può essere ottenuto con qualsiasi numero e il suo contrario, come 8 e -8 (per entrambi, il risultato è 64).

Questo non è possibile con esempi come quello dei paesi e dei loro continenti, ma questo non vuol dire che al di fuori della matematica non ci siano relazioni meno rigide o, per così dire, più flessibili. Se pensiamo a un insieme in cui sono elencati i nomi di dieci persone e un altro, il loro codominio, in cui sono elencati alcuni dei loro amici, sarebbe possibile che per ogni elemento del secondo insieme ce ne sia più di uno del dominio.

Tornando al dominio dei numeri, se volessimo modificare la funzione di cui sopra per farla diventare iniettiva dovremmo solo restringere il dominio ai numeri reali positivi: in questo modo, mai più un elemento di uno degli insiemi sarebbe legato a più di uno dell'altro.

La definizione formale di una funzione iniettiva è la seguente: f: X -> Y è iniettiva solo se per gli elementi dell'insieme X a e b è soddisfatto che f(a) è uguale a f(b) quando a è uguale a b. In altre parole, la funzione è anche iniettiva se quando gli elementi sono diversi, lo sono anche le loro immagini.

D'altra parte, se abbiamo due insiemi tra i quali esiste una funzione iniettiva, si parla di cardinalità quando gli elementi del primo sono minori o uguali alle loro immagini. Se una seconda funzione mette in relazione gli insiemi nella direzione inversa, allora diremo che c'è un'applicazione biiettiva tra gli insiemi.