Numeri complessi

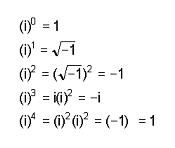
I numeri complessi sono un gruppo di cifre risultanti dalla somma di un numero reale e un numero immaginario. Un numero reale, secondo la definizione, è un numero che può essere espresso da un numero intero (4, 15, 2686) o decimale (1,25; 38,1236; 29854,152). D'altra parte, un numero immaginario è un numero il cui quadrato è negativo. Il concetto di numero immaginario è stato sviluppato da Leonhard Euler nel 1777, quando ha dato a v-1 il nome i (da "immaginario").

La nozione di numero complesso nasce dall'impossibilità dei numeri reali di comprendere le radici di ordine pari dell'insieme dei numeri negativi. I numeri complessi possono quindi riflettere tutte le radici dei polinomi, cosa che i numeri reali non sono in grado di fare.

Grazie a questa peculiarità, i numeri complessi sono utilizzati in vari campi della matematica, della fisica e dell'ingegneria. A causa della loro capacità di rappresentare la corrente elettrica e le onde elettromagnetiche, per esempio, sono frequentemente utilizzati in elettronica e nelle telecomunicazioni. La cosiddetta analisi complessa, cioè la teoria delle funzioni di questo tipo, è considerata una delle sfaccettature più ricche della matematica.

Si noti che il corpo di ogni numero reale consiste di coppie ordinate (a, b). La prima componente (a) è la parte reale, mentre la seconda componente (b) è la parte immaginaria. I numeri immaginari puri sono quelli che consistono solo della parte immaginaria (quindi a=0).

I numeri complessi costituiscono il cosiddetto corpo complesso (C). Quando la componente reale a viene identificata con il corrispondente complesso (a, 0), il corpo di questi numeri reali (R) si trasforma in un sotto corpo di C. Inoltre, C forma uno spazio vettoriale bidimensionale su R. Questo dimostra che i numeri complessi non ammettono la possibilità di mantenere un ordine, a differenza dei numeri reali.

Storia dei numeri complessi

A partire dal I secolo a.C., alcuni matematici greci, come Erone di Alessandria, iniziarono ad abbozzare il concetto di numeri complessi, di fronte alle difficoltà nella costruzione di una piramide. Tuttavia, non fu fino al XVI secolo che cominciarono ad occupare un posto importante nella scienza; a quel tempo, un gruppo di persone cercava formule per ottenere le radici esatte dei polinomi di grado 2 e 3.

In primo luogo, il loro interesse era trovare le radici reali delle equazioni sopra menzionate; tuttavia, dovevano anche occuparsi delle radici dei numeri negativi. Fu il famoso filosofo, matematico e fisico francese Cartesio a creare il termine numeri immaginari nel XVII secolo, e solo più di 100 anni dopo il concetto di numeri complessi sarebbe stato accettato. Tuttavia, ci volle lo scienziato tedesco Gauss a riscoprirlo qualche tempo dopo perché ricevesse l'attenzione che meritava.

Il piano complesso

Per interpretare geometricamente i numeri complessi, è necessario utilizzare un piano complesso. Nel caso della loro somma, questa può essere correlata a quella dei vettori, mentre la loro moltiplicazione può essere espressa da coordinate polari, con le seguenti caratteristiche:

* la grandezza del loro prodotto è la moltiplicazione delle grandezze dei termini;

* l'angolo dall'asse reale del prodotto è la somma degli angoli dei termini.

Quando si rappresentano le posizioni dei poli e degli zeri di una funzione in un piano complesso, si usano spesso i cosiddetti diagrammi di Argand.