Del teorema di Pitagora

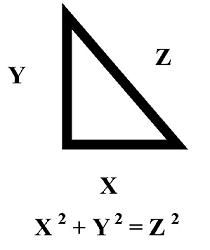
Si chiama teorema una proposizione che può essere dimostrata logicamente da un presupposto o da altri teoremi già dimostrati. In questo contesto, è essenziale rispettare alcune regole di inferenza per arrivare a questa dimostrazione.

Pitagora di Samo (582 a.C-507 a.C.), inoltre, era un filosofo e matematico di origine greca. Contrariamente a quanto si potrebbe supporre, Pitagora non fu colui che creò il teorema che porta il suo nome. Questo teorema fu sviluppato e applicato molto prima in Babilonia e in India; tuttavia, la scuola pitagorica (e non Pitagora) fu un pioniere nel trovare una dimostrazione formale per questo teorema.

Pitagora può anche dire che è considerato il primo matematico puro della storia e ha fortemente contribuito allo sviluppo di aree scientifiche come la matematica sopra menzionata ma anche la geometria, l'aritmetica, l'astronomia e la musica. E tutto grazie sia al suo suddetto teorema che ad altre importanti scoperte come il significato funzionale dei numeri o l'incommensurabilità dei lati e della diagonale di quello che è il quadrato.

Specificamente, si può dire che il secondo teorema di Pitagora sottolinea che il quadrato dell'ipotenusa, nei triangoli rettangoli, è uguale all'ombra dei quadrati delle gambe. Per capire questa frase, bisogna tener presente che un triangolo che si identifica come un rettangolo è un triangolo che ha un angolo retto (cioè misura 90º), che l'ipotenusa è costituita dal lato più lungo di questa figura (e opposto all'angolo retto) e che le gambe sono caratterizzate dall'essere i due lati più piccoli del triangolo rettangolo.

L'importanza di questo teorema che ci interessa ora è che ci permette di scoprire una misura basata su due dati specifici. In altre parole, è stato un passo importante nel campo della matematica perché ha dimostrato che conoscendo le lunghezze di due lati di un triangolo rettangolo possiamo scoprire qual è la lunghezza del terzo lato.

Nel 1927, il matematico ES Loomis raccolse più di 350 prove del teorema di Pitagora. Loomis ha classificato queste dimostrazioni in quattro gruppi: dimostrazioni geometriche, che sono fatte sulla base del confronto delle zone; dimostrazioni algebriche, sviluppate sulla base della relazione tra i lati e i segmenti del triangolo; dimostrazioni dinamiche, che fanno appello alle proprietà della forza; e dimostrazioni quaternioniche, che risultano dall'uso dei vettori.

Nel caso delle dimostrazioni geometriche, è stato notato che ci sono molti autori o scienziati che le hanno eseguite nel corso della storia. Tra questi si evidenziano, per esempio, il grande filosofo Platone, che li ha sviluppati nei suoi famosi dialoghi, o il matematico Euclide.

Quelle algebriche hanno portato anche vari personaggi ad aver deciso, in un modo o nell'altro, di elevarli, svilupparli e dimostrarli in modo reale e palpabile. Pertanto, in questo caso, sarebbe necessario menzionare figure illustri come Leonardo da Vinci, che ha perseguito la costruzione e la dimostrazione di questa forma del suddetto Teorema di Pitagora.