Vettore risultante

Nel contesto della fisica, una quantità si chiama vettore quando è definita dal suo indice, dal suo punto di applicazione, dalla sua importanza e dal suo significato. Sulla base delle loro caratteristiche è possibile parlare di diverse classi di vettori.

In latino troviamo l'origine etimologica di questo termine, che deriva da "vector - vectoris", che può essere tradotto come "colui che guida".

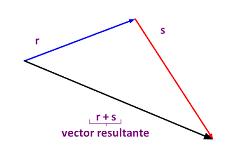
L'idea del vettore risultante può apparire quando l'operazione Sum con i vettori. Con il cosiddetto metodo poligonale, i vettori da aggiungere devono essere tracciati su un grafico, facendo coincidere l'origine di ogni vettore con la fine del vettore successivo. È chiamato vettore risultante al vettore che ha origine coincidente con il primo vettore e termina alla fine del vettore situato nell'ultimo posto.

VR è l'acronimo usato per riferirsi al vettore risultante che, come il resto dei vetttori, quando viene analizzato richiede che vengano presi in considerazione tre elementi che lo modellano. Ci riferiamo a quanto segue:
- Il modulo, che serve a indicare l'intensità della sua grandezza ed è rappresentato dalla dimensione del vettore.
- La direzione, che si riferisce alla pendenza della linea.
- Il significato, che ha la particolarità di essere rappresentato da quella che è la punta della frequenza del vettore in questione.

L'addizione dei vettori attraverso questo metodo coinvolge diversi vettori, facendoli unire dalle loro estremità. Quindi, prenderemo un vettore e lo metteremo accanto ad un altro, in modo che l'origine dell'uno sia unita all'altro. Il vettore risultante "nasce" all'origine del primo vettore che prendiamo e "finisce" alla fine del vettore che mettiamo nell'ultimo spazio.

Si tenga presente che, per aggiungere vettori con il metodo poligonale, è essenziale non modificare la proprietà dei file - i vettori devono solo essere traslati.

È importante tenere presente che, quando si tratta di poter imparare questa materia che ci governa, quello che dobbiamo fare è tornare ad alcuni elementi fondamentali della matematica e dell'algebra. Ci riferiamo alle coordinate X e Y. Fondamentalmente, è da questi e dalle loro ombre corrispondenti che si otterrà il vettore risultante.

Parliamo anche di un vettore risultante in riferimento a quello che, in un sistema, genera lo stesso effetto dei vettori che lo compongono. Il vettore che ha la stessa direzione e dimensione ma la direzione opposta è classificato come vettore equilibrante.

Questo vettore equilibrante di cui sopra, che si chiama anche VE, come abbiamo detto, ha la direzione opposta, è opposto in quello che è 180º.
Oltre a quelli menzionati, ci sono molti altri tipi di vettori, come complanari, paralleli, opposti, concorrenti, collineari, fissi...