Valore assoluto

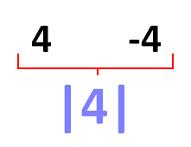
La nozione di valore assoluto è usata in matematica per nominare il valore che un numero ha oltre il suo segno. Ciò significa che il valore assoluto, noto anche come modulo, è la grandezza numerica del numero indipendentemente dal fatto che il suo segno sia positivo o negativo.

Prendiamo il caso del valore assoluto 5. Questo è il valore assoluto sia di +5 (5 positivo) che di -5 (5 negativo). Il valore assoluto, in breve, è lo stesso nel numero positivo e nel numero negativo: in questo caso, 5. Bisogna notare che il valore assoluto è scritto tra due barre verticali parallele; quindi, la notazione corretta è |5|.

La definizione del concetto indica che il valore assoluto è sempre uguale o maggiore di 0 e non è mai negativo. Da quanto sopra, possiamo aggiungere che il valore assoluto dei numeri opposti è lo stesso; 8 e -8 condividono quindi lo stesso valore assoluto: |8|.

Il valore assoluto può anche essere inteso come la distanza tra il numero e 0. Il numero 563 e il numero -563 sono, su una linea dei numeri, alla stessa distanza da 0. Questo, quindi, è il valore assoluto di entrambi: |563|.

La distanza tra due numeri reali, invece, è il valore assoluto della loro differenza. Tra 8 e 5, per esempio, c'è una distanza di 3. Questa differenza ha un valore assoluto di |3|.

Il concetto di valore assoluto è presente in diversi argomenti della matematica, e il vettore è uno di questi; più precisamente, è nella norma vettoriale che ci troviamo di fronte a una definizione simile. Prima di continuare, però, è necessario definire lo spazio euclideo, dato che questi concetti sono coniugati in questo ambito.

Lo spazio euclideo è inteso come un tipo di spazio geometrico in cui gli assiomi di Euclide sono soddisfatti. Un assioma è una proposizione la cui chiarezza è tale da non richiedere prove per essere ammessa; nello specifico, nel campo della matematica, sono così chiamati i principi fondamentali e indimostrabili su cui si costruiscono le teorie.

Euclide, intanto, nacque in Grecia nel 325 a.C. circa, e la sua dedizione ai numeri gli valse il titolo di "padre della geometria". La sua opera più importante è una raccolta di tredici libri raggruppati sotto il titolo "Elementi", dove vengono presentati i suddetti assiomi (noti anche come postulati di Euclide), e che vedremo brevemente di seguito:

1) se prendiamo due punti qualsiasi, è possibile unirli per mezzo di una linea retta;

2) è possibile prolungare continuamente tutti i segmenti, indipendentemente dalla direzione;

3) i cerchi possono avere origine da qualsiasi punto, che sarà preso come centro, e il loro raggio può assumere qualsiasi valore;

4) qualsiasi coppia di angoli retti è congruente;

5) è possibile tracciare una sola linea parallela a un'altra da un punto esterno a quest'ultima.

Data la base degli spazi euclidei, possiamo dire che i vettori possono essere rappresentati in essi sotto forma di segmenti orientati tra due punti qualsiasi. Se prendiamo un vettore, possiamo definire la sua norma come la distanza che esiste tra due punti, che servono da limite; tanto che in uno spazio euclideo questa norma corrisponde al modulo, cioè alla lunghezza di questo vettore.

Come il valore assoluto, il modulo di un vettore è sempre un numero positivo o zero, poiché rappresenta una lunghezza, una distanza. In questo caso, come in molti altri, associare questa grandezza a un segno potrebbe causare complicazioni inutili.

Nel campo della programmazione dei videogiochi, invece, il valore assoluto può apparire in numerose occasioni, a seconda della metodologia di ogni sviluppatore. Per esempio, quando si calcola la velocità attuale di un personaggio, possiamo ignorare la direzione in cui il personaggio si sta muovendo e guardare semplicemente il segmento tra 0 e la velocità massima, applicando l'accelerazione di conseguenza; infine, basta moltiplicare il valore risultante per il vettore direzione del personaggio per tradurlo.