Prodotti degni di nota

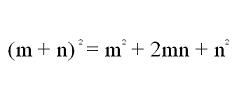
Se ci concentriamo sul linguaggio colloquiale, potremmo affermarlo prodotti notavoli sono quelle merci che possono essere acquistate sul mercato e che hanno caratteristiche speciali: un'auto di lusso, un orologio d'oro, un computer di ultima generazione ...

La nozione di prodotti notevoliTuttavia, di per sé non si riferisce a questo dominio, ma è usata nel file matematico per citare alcune espressioni algebriche può rendere immediatamente possibile risalire ad un processo in modo più dettagliato.

In questo senso, dobbiamo ricordare che il concetto di prodotto, in campo matematico, si riferisce al risultato di un'operazione di moltiplicazione. I valori che entrano in gioco in queste operazioni, invece, sono noti come fattori.

Un'espressione algebrica che è frequentemente verificata e che può essere composta in forma annodata è quindi chiamata prodotto notevole. Un binomio quadratico e il prodotto di due binomi connessi sono esempi di prodotti notevoli.

Un esempio concreto di un binomio quadratico è il seguente:

(m + n) ² = m² + 2mn + n²

Detto prodotto notevole si riferisce al quadrato della somma di m e n è uguale al quadrato di m più due volte m moltiplicato per n più il quadrato di n.

Possiamo verificarlo sostituendo i termini con valore numerico:

(2 + 4) ² = 2² + 2 x 2 x 2 x 4 + 4²
6² = 4 + 16 + 16 + 16
36 = 36

In questo modo, se troviamo il quadrato di un binomio come nell'esempio precedente, possiamo fattorizzarlo immediatamente, senza dover ricorrere a tutti i passaggi, poiché è un prodotto notevole.

La combinazione quadrata può anche consistere nella sottrazione delle due variabili che sono quadrate. In questo caso, la differenza rispetto all'esempio precedente è che per risolverlo, il primo seno più dopo il simile, in modo che la seguente equazione:

(m - n) ² = m² - 2mn + n²

Oltre al quadrato binomiale, i prodotti notevoli sono divisi nelle seguenti tipologie (le equazioni possono essere viste nell'immagine):

* Somma binomiale per differenza binomiale: è il prodotto tra un binomio in cui vengono sommate le sue variabili e un altro in cui vengono sottratte. Per risolverlo, basta sottrarre il quadrato di ogni variabile;

* Cubo binomiale: oltre al binomio quadratico, si divide anche in addizione e sottrazione. Nel primo caso, è il cubo della somma di due variabili, che è uguale al primo quadrato più tre volte il primo quadrato per il secondo, più tre volte il primo tempo il secondo quadrato, più il secondo cubo. . Per la sottrazione, il primo e l'ultimo devono essere invertiti ancora una volta;

* Ombra del cubo: quando si osserva il prodotto tra l'ombra di due varianti, e il primo quadrato meno il primo per il secondo più il secondo quadrato, c'è un modo molto semplice di risolverlo, che consiste nell'aggiungere il cubo della prima variante alla seconda.

Per quanto riguarda le applicazioni dei prodotti di nota, è ovvio che non si trovano nella vita quotidiana della maggior parte delle persone, come è il caso, per esempio, della semplice regola dei tre, tra gli altri strumenti matematici più accessibili. Tuttavia, i professionisti di vari settori beneficiano dei prodotti di nota; vediamo tre esempi qui sotto:

* gli ingegneri e gli ingegneri civili lo usano per misurare distanze, volumi e aree;
* si usa per calcolare l'intensità della corrente elettrica;
* permette di stimare il numero di individui trovati in un algoritmo genetico;
* si usa per calcolare la torsione di varie strutture.