Polinomio

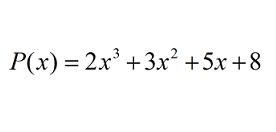
Le espressioni algebriche formate dall'unione di due o più variabili e costanti, legate da operazioni di moltiplicazione, sottrazione o addizione, sono chiamate polinomi. L'aggettivo polinomiale, invece, si applica alla quantità o alle operazioni che possono essere espresse come polinomi.

Grazie ai polinomi, è possibile sviluppare diversi calcoli e avvicinarsi a una funzione derivabile. Molte scienze usano i polinomi nei loro studi e ricerche, dalla chimica e la fisica all'economia.

Per aggiungere o sottrarre polinomi, è necessario raggruppare i diversi monomi e semplificare quelli che sono simili. La moltiplicazione, invece, si effettua moltiplicando i termini di un polinomio per i termini dell'altro, semplificando infine i monomi che sono simili.

È importante notare che i polinomi non sono infiniti, cioè non possono essere composti da un numero infinito di termini. D'altra parte, la divisione è un'operazione che non fa mai parte dei polinomi.

Una proprietà dei polinomi è che, quando vengono aggiunti, sottratti o moltiplicati, il risultato sarà sempre un altro polinomio. Quando il polinomio ha due termini, si chiama binomio. Se ha tre termini, d'altra parte, si chiama un trinomio.

Un altro concetto rilevante quando si lavora con i polinomi è la nozione di grado. Il grado del monomio è il massimo esponente della sua variabile: il grado del polinomio, quindi, sarà il grado del suo monomio con il valore più alto.

Il polinomio di Taylor è un teorema enunciato nella prima decade del XVIII secolo dal matematico Brook Taylor, originario della Gran Bretagna, ma scoperto alla fine del secolo precedente da un matematico e astronomo scozzese di nome James Gregory. Utilizzandola nello studio di una funzione, è possibile trovare approssimazioni polinomiali in un ambiente in cui può essere differenziata, e utilizzare questa stima per la delimitazione dell'errore.

Il tipo di ambiente utilizzato per l'applicazione del polinomio di Taylor è ridotto, il che significa che si prende in considerazione un certo numero di punti intorno a un principale, in modo che si possa contare su un certo margine ma non sia eccessivo. I coefficienti del polinomio dipendono dalle derivate della funzione (una misura della velocità con cui un valore cambia quando la sua variabile dipendente viene modificata) in quel punto.

Il metodo chiamato interpolazione polinomiale, invece, viene utilizzato per approssimare i valori assunti da una funzione data, di cui si conosce semplicemente l'immagine in un numero finito di ascissa (coordinate cartesiane). In generale, solo i valori presi per le ascisse sono disponibili (in altre parole, l'espressione della funzione è sconosciuta).

Con questo metodo, l'obiettivo è quello di trovare un polinomio che approssimi anche altri valori che non sono noti con un particolare livello di precisione, per cui esiste la formula dell'errore di interpolazione, che serve a regolare la precisione.

Il termine polinomio primitivo sta per due concetti: un polinomio di una struttura algebrica (chiamato dominio di fattorizzazione unica) in cui tutti i suoi elementi possono essere decomposti solo come prodotto di elementi primi, tali che i suoi coefficienti abbiano 1 come maggior divisore comune; per un'estensione di corpi, il polinomio minimo di uno dei suoi elementi primitivi.

Questo ci porta al concetto di polinomio minimo che, in matematica, si riferisce al polinomio normalizzato (il cui coefficiente primo è 1) di grado più piccolo tale che il suo risultato sia 0.