Poliedri

I poliedri sono elementi geometrici che hanno facce piane e che contengono un volume che non è infinito. La radice etimologica del termine, che si trova nella lingua greca, si riferisce a "molte facce".

Un poliedro può essere inteso come un corpo solido tridimensionale. Quando tutte le sue facce e gli angoli sono uguali tra loro, si chiama poliedro regolare. Altrimenti, è un poliedro irregolare.

Un'altra possibile classificazione è legata al numero di facce che ha. Un poliedro a sei lati è chiamato esaedro, un poliedro a cinque lati è conosciuto come pentaedro, e così via, il nome è sempre formato dal prefisso greco corrispondente (hexa, penta, tetra, ecc.).

Si può anche fare una distinzione tra poliedri concavi e poliedri convessi. I poliedri concavi sono quelli che, quando si uniscono due punti all'interno del corpo, il segmento corrispondente esce dalla superficie. Nei poliedri convessi, invece, i segmenti che collegano due punti nello spazio interno non lasciano mai il corpo geometrico.

Un esempio di poliedro è il cubo, un poliedro regolare con quattro facce uguali, i cui angoli interni sono congruenti tra loro. Ciò significa che i dadi costruiti in questo modo sono poliedri. Anche le scatole le cui facce sono quadrate rientrano nel gruppo dei poliedri.

Un altro esempio di poliedro sono i prismi: in questo caso, sono poliedri irregolari. È importante notare che le classificazioni non sempre si escludono a vicenda. Il prisma è un poliedro irregolare, ma è anche un poliedro convesso.

I poliedri sono classificati in diverse famiglie, due delle quali sono elencate di seguito:

* Solidi platonici: sono quelli che hanno facce e angoli uguali e sono convessi. Ci sono solo cinque poliedri in questa famiglia, che sono il cubo, il dodecaedro, il tetraedro, l'ottaedro e l'icosaedro. Questa famiglia è essenziale, poiché altre derivano da essa, come i solidi archimedei;

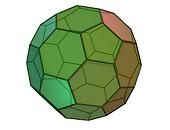
* solidi archimedei: sono convessi, i loro vertici sono uniformi e le loro facce sono regolari (ma non uniformi). Ce ne sono solo undici, e alcuni di essi sono ottenuti troncando quelli platonici, cioè tagliando i loro vertici o i loro bordi. Alcuni dei solidi archimedei sono il cubo troncato, il rombicubottaedro, il rombicosidodecaedro e l'icosidodecaedro troncato;

Un poliedro i cui vertici corrispondono al centro delle facce di un secondo poliedro è noto come poliedro duale. Ecco alcuni fatti curiosi: il poliedro duale di un poliedro duale assomiglia all'originale; il duale di un poliedro con vertici equivalenti ha anche facce equivalenti; il duale di un poliedro che ha bordi equivalenti avrà anche facce equivalenti. Associati a questa classificazione sono i solidi di Keplero-Poinsot e platonici, tra altri poliedri regolari.

Sebbene si possano riconoscere diversi tipi di dualità da cui mettere in relazione due figure, tra le più usate ci sono la reciprocità polare e la dualità topologica. Vediamo ora la definizione di questi concetti:

* reciprocità polare: in generale, per definire la dualità parlando della sua reciprocità polare, si prende come riferimento una sfera concentrica, in modo che ogni polo (o vertice) sia associato a una faccia e al suo piano (detto polare), in modo tale che la linea immaginaria passante per il vertice e il centro sia perpendicolare a questo piano e il quadrato del raggio possa essere ottenuto se si effettua il prodotto delle distanze da ogni lato al centro;

* dualità topologica: quando un poliedro duale è distorto in modo che non può più essere ottenuto per reciprocità, il poliedro originale e quello attuale possono essere detti topologicamente duali, ma non reciproci polari.