Prodotto puntuale

Nel campo della matematica, il risultato di una moltiplicazione è chiamato prodotto. L'idea di sale, a breve termine, può essere usata per denotare il numero che permette di descrivere un fenomeno con grandezza, semplicemente tracciando la direzione del vettore.

È importante considerare prima di procedere che un vettore è una grandezza che richiede di considerare, oltre alla sua quantità, il suo significato, la direzione e il punto di applicazione.

Si chiama prodotto scalare, in questo quadro, l'operazione algebrica che parte da due sequenze numeriche di uguale lunghezza (che hanno solo la forma di vettori) e arriva ad un solo numero.

Chiamato anche Punto prodotto, prodotto interno o Prodotto interno, il prodotto scalare si ottiene aggiungendo il prodotto degli input di una coppia di sequenze numeriche. Il risultato non è un vettore, ma uno scalare.

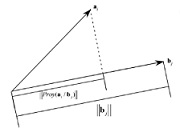
Si può affermare che il prodotto scalare di un vettore a→ e un vettore b→ (a → ⋅ b →) restituisce un numero (la salita) tale che a → ⋅ b → = (a →) ⋅ (b →) ⋅ cos (α)Essere α l'angolo che compone i due vettori (a→ e b→).

Questo ci permette di sostenere che, per la geometria, il prodotto di punti è la moltiplicazione delle dimensioni euclidee di due vettori e il coseno dell'angolo formato da entrambi.

Se i vettori sono paralleli e condividono la stessa direzione, il prodotto scalare è equivalente alla moltiplicazione dei moduli. Se invece la direzione è diversa, si ottiene moltiplicando i suoi moduli ma sottraendo il segno negativo.

Nel caso di vettori perpendicolari, l'angolo formato è 90º e il prodotto scalare è uguale a 0.