Onda trasversale

In fisica, un'onda è un moto periodico la cui propagazione può avvenire nel vuoto o in un mezzo fisico. Trasversale, invece, è un aggettivo che allude a ciò che si allontana dalla direzione retta, che attraversa perpendicolarmente o che viene attraversato.

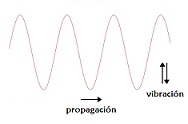
Un'onda trasversale, in questo quadro, è quella che presenta una grandezza vettoriale con oscillazioni in una direzione perpendicolare alla direzione di propagazione. Questa caratteristica le distingue dalle onde longitudinali, che oscillano nella stessa direzione dello spostamento dell'onda.

Per comprendere la nozione di onda trasversale, è essenziale ricordare che la propagazione delle onde in un mezzo è legata alla vibrazione che provocano nelle particelle del mezzo in questione. Quando la direzione di propagazione è perpendicolare alla direzione in cui vibrano queste particelle, si tratta di un'onda trasversale. Al contrario, se la direzione di propagazione è la stessa della direzione in cui vibrano le particelle del mezzo, l'onda è longitudinale.

Le onde elettromagnetiche, per esempio, sono onde trasversali. Così come le onde che si generano sulla superficie dell'acqua se lanciamo un oggetto contundente, per citare un altro caso.

Supponiamo di lanciare un sasso in un lago e che atterri vicino a dove galleggia una boa. La direzione della vibrazione prodotta sulla superficie è perpendicolare alla direzione dello spostamento dell'onda. La boa, nel frattempo, sale e scende secondo l'arrivo dei fronti d'onda, che avanzano orizzontalmente. L'azione alla fine ha portato alla comparsa di onde trasversali.

C'è un concetto generalmente noto come onde trasversali su una corda, e si concentra proprio sul moto ondoso che si propaga in una corda che è sottoposta a una tensione. Uno degli obiettivi che si presentano in problemi di questo tipo, nel campo della fisica, è scoprire la velocità di propagazione delle onde, e per questo è necessario trovare la formula appropriata.

Per spiegare questo argomento vedremo di seguito un esempio in cui passeremo attraverso ciascuna delle variabili e alla fine arriveremo all'equazione che ci permette di calcolare la velocità di propagazione delle onde trasversali in una corda. Prendiamo per esempio una corda con una certa tensione, che rappresenteremo con la variabile T. Quando è in equilibrio, possiamo dire che la linea che forma è retta.

Se, invece, spostiamo un elemento di lunghezza dx da un punto di cui conosciamo la posizione sull'asse X e lo facciamo di una grandezza ψ (la ventitreesima lettera greca, psi) prendendo come riferimento la sua posizione di equilibrio. Per calcolare l'accelerazione dell'elemento dobbiamo applicare la seconda legge di Newton, conosciuta anche come la legge fondamentale della dinamica:

"il moto cambia in proporzione diretta alla forza impressa e lo fa secondo la retta su cui è impressa".

La tensione è uguale alla forza che il lato sinistro della corda esercita sullo stesso lato dell'elemento, e in questo punto la direzione è tangente alla corda, dando luogo a un angolo che chiamiamo α. Lo stesso si può dire per il lato destro, tranne che l'angolo formato si chiama α'. Poiché l'elemento si sta muovendo verticalmente, l'equazione di cui abbiamo bisogno per risolvere il problema è la seguente: velocità = √tensione / densità lineare.