Gradiente

Prima di entrare nel significato del termine gradiente, procediamo a conoscere la sua origine etimologica. In questo caso, possiamo sottolineare che è una parola che deriva dal latino, esattamente da "gradiens, gradientis", che può essere tradotto come "che scende" o "che fa dei passi".

Inoltre, dobbiamo indicare che è un tecnicismo che è stato creato nel campo della fisica.

È anche interessante sapere che in fisica è molto comune parlare del Laplaciano, che è la divergenza del gradiente.

La nozione di gradiente è usata in fisica per riferirsi al rapporto tra il cambiamento del valore di una quantità in due punti e la distanza tra essi. Il gradiente può essere la differenza di intensità di un'energia o di un effetto in due momenti o punti diversi.

Il gradiente di concentrazione, in questo quadro, è la quantità che riflette in quale proporzione e direzione si verifica il cambiamento più importante nella concentrazione di un soluto che è dissolto in una soluzione non omogenea. Si tratta, in altre parole, di una differenza di concentrazione.

Per quanto riguarda le membrane cellulari, il gradiente di concentrazione si riferisce alla differenza di concentrazione di ioni che si trova in diversi punti della membrana in questione.

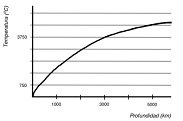
Il gradiente di temperatura o gradiente termico, invece, si riferisce al cambiamento di temperatura per unità di distanza. Quando si registra un gradiente di temperatura, c'è un trasferimento di calore dal corpo che è più caldo al corpo che è più freddo.

C'è anche il gradiente di pressione o gradiente barometrico, che è prodotto dalla differenza di pressione che si registra in un fluido. Di solito si riferisce alla variazione di pressione per unità di profondità.

Allo stesso modo, bisogna anche notare che il termine in questione è ampiamente utilizzato nel campo della matematica. In questo caso, è usato come sinonimo di una funzione di valore di tipo vettoriale, che è quindi una funzione scalare.

In questo campo è anche conosciuto con il nome di vettore gradiente e ha caratteristiche quali che diventa anulare in quelli che sono i punti di tipo stazionario e che diventa di classe ortogonale rispetto alle cosiddette superfici equiscalari. Inoltre, dobbiamo aggiungere il fatto che punta verso la direzione in cui la derivata direzionale è massima.

È interessante sapere che per facilitare il calcolo dei gradienti e delle derivate parziali esistono calcolatori online che permettono di realizzare queste operazioni in modo rapido e con totale precisione.

Un gradiente, infine, è un pendio o una pendenza. Può essere una pendenza generata da un certo grado di inclinazione. In questo caso, il gradiente di solito riflette il rapporto tra la distanza orizzontale e la distanza verticale.