Simmetria assiale

La simmetria, concetto derivato dal latino symmetrĭa, si riferisce alla corrispondenza tra la posizione, la forma e la dimensione dei componenti di un insieme. Assiale, invece, è quello che è legato a un asse (la parte che fa da supporto a qualcosa e che, in certi contesti, permette a un dato oggetto di ruotare).

La simmetria assiale è la simmetria che esiste intorno a un asse quando tutti i semipiani presi da una data bisettrice presentano le stesse caratteristiche.

Per determinare se esiste una simmetria assiale, si considerano i punti che appartengono a una figura coincidenti con i punti che fanno parte di un'altra figura, prendendo come riferimento l'asse di simmetria (una linea). In questo modo, la simmetria assiale comporta un fenomeno simile a quello che si verifica quando uno specchio riflette un'immagine.

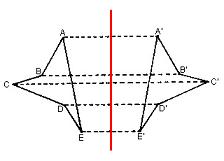
Con la simmetria assiale, le figure simmetriche hanno punti omologhi: il punto A di una figura è omologo al punto A' dell'altra figura; il punto B di una figura è omologo al punto B' dell'altra figura; e così via. La distanza tra i diversi punti appartenenti alla figura originale, d'altra parte, è identica alla distanza tra i punti nella figura simmetrica in questione.

È importante ricordare che il concetto di simmetria assiale è utile in fisica. Quando si parte da dati a simmetria assiale, anche la soluzione di certe incognite ha una simmetria assiale, una caratteristica che permette di ridurre le variabili del problema.

Come disegnare la simmetria assiale di un poligono?

Se la teoria fondamentale della simmetria assiale non è particolarmente complessa, è sempre utile mettere in pratica le conoscenze, in modo da poterle interiorizzare meglio. In questo caso particolare, abbiamo il vantaggio della sua compatibilità con il disegno, qualcosa che la maggior parte delle persone può fare con una certa facilità. Pertanto, vedremo di seguito una serie di passi per ottenere una figura simmetrica ad un'altra.

Prima di tutto, è necessario disegnare una figura e determinare i punti che la compongono. Per questo esempio useremo un poligono con quattro vertici (A, B, C e D), anche se i passi funzionano per qualsiasi altro caso. Avendo tracciato il poligono e definito correttamente i suoi vertici, viene il passo più importante: stabilire la posizione e l'orientamento dell'asse di simmetria.

Anche se negli esempi più semplici siamo abituati a vedere assi di simmetria assiale perpendicolari al suolo, che ci danno una figura accanto all'altra, è necessario sottolineare che l'angolo di questo asse è indifferente. Per capire questo, possiamo pensare all'asse come a uno specchio che vogliamo usare per riflettere un oggetto: non importa se lo mettiamo davanti, dietro o a lato dell'oggetto, e non importa se lo ruotiamo, perché farà sempre il suo lavoro con successo. Infatti, l'asse può passare per uno dei punti della figura originale, se vogliamo un risultato in cui entrambi si toccano.

Una volta disegnato l'asse di simmetria assiale, possiamo iniziare a disegnare i punti della nuova figura. Per fare questo, dobbiamo misurare la distanza da ciascuno dei vertici originali e l'asse, lungo una linea perpendicolare ad esso, e poi percorrere la stessa distanza dall'altra parte dell'asse fino a trovare la posizione omologa. Poiché la nostra figura ha solo quattro punti, questo è un compito relativamente semplice.

Con i quattro vertici omologhi, che chiameremo A', B', C' e D', non resta che tracciare ciascuno dei lati corrispondenti.