Trigonometria

Il primo passo prima di entrare pienamente nell'analisi del significato della parola trigonometria è quello di procedere allo stabilimento della sua origine etimologica. In questo senso dobbiamo esporre che quello menzionato si trova nel greco dove possiamo osservare come è formato dall'unione di trigonon che equivale a "triangolo", metron che può essere definito come "misura" e tria che è sinonimo di "tre".

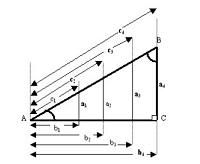
La trigonometria è la suddivisione della matematica che si occupa del calcolo degli elementi dei triangoli. Lo fa studiando le relazioni tra gli angoli e i lati dei triangoli.

Questa specialità è coinvolta in diverse aree della matematica dove è necessario un lavoro di precisione. La trigonometria, tuttavia, ha una grande varietà di applicazioni. Permette, per esempio, di misurare le distanze tra due luoghi o corpi celesti utilizzando tecniche di triangolazione. La trigonometria è anche applicata nei sistemi di navigazione satellitare.

Ci sono tre unità utilizzate dalla trigonometria per la misura degli angoli: il radiante (considerato l'unità naturale degli angoli, afferma che una circonferenza completa può essere divisa in 2 pi radianti), il gradiano o grado centesimale (che permette di dividere la circonferenza in quattrocento gradi centesimali) e il grado sessagesimale (usato per dividere la circonferenza in trecentosessanta gradi sessagesimali).

I principali rapporti trigonometrici sono tre: il seno (che consiste nel calcolare il rapporto tra la gamba opposta e l'ipotenusa), il coseno (un altro rapporto ma, in questo caso, tra la gamba adiacente e l'ipotenusa) e la tangente (il rapporto tra le due gambe: quella opposta su quella adiacente).

I rapporti trigonometrici reciproci, invece, sono la cosecante (il rapporto reciproco del seno), la secante (il rapporto reciproco del coseno) e la cotangente (il rapporto reciproco della tangente). In particolare, ci riferiamo ai rapporti trigonometrici di un angolo qualsiasi.

Questo ci porterebbe a parlare della cosiddetta circonferenza goniometrica, caratterizzata dal fatto che il suo raggio è l'unità stessa e il suo centro non è altro che l'origine delle relative coordinate. Tutto questo senza dimenticare che gli assi delle coordinate delimitano quattro quadranti che sono numerati in senso contrario a quello orario.

Un'identità trigonometrica è nota come un'uguaglianza che coinvolge funzioni trigonometriche che sono verificabili per qualsiasi valore delle variabili (gli angoli a cui le funzioni sono applicate).

In aggiunta a quanto sopra, non possiamo trascurare l'esistenza di due tipi di trigonometria. Così, in primo luogo, avremmo la cosiddetta trigonometria sferica, che è quella parte della matematica che si concentra sullo studio dei triangoli sferici.

In secondo luogo, esiste anche la cosiddetta trigonometria piana. In questo caso, come indica il suo nome, è la scienza che ha come oggetto di analisi e studio i vari triangoli piani.