Topologia

Il termine topologia è usato per identificare un'area della matematica che studia la continuità e altri concetti che derivano da essa. È una specializzazione legata alle proprietà e alle caratteristiche che i corpi geometrici possiedono e che rimangono invariati da cambiamenti continui, indipendentemente dalla loro dimensione o aspetto.

Si noti che le funzioni continue in matematica sono quelle che, in punti vicini del dominio, sperimentano piccole variazioni di valori. Graficamente, queste funzioni possono di solito essere disegnate senza dover sollevare la matita dal foglio.

Un altro concetto centrale della topologia è lo spazio topologico, una struttura matematica che permette di definire in modo formale la continuità, la connettività e la convergenza, tra altri concetti.

Topologia, quindi, è la specializzazione che si concentra sullo studio delle funzioni continue e degli spazi topologici. Questa disciplina lavora con gli oggetti in vari modi, purché la continuità non sia interrotta. Nel linguaggio comune, si potrebbe dire che la topologia permette di piegare, allungare, torcere o restringere gli elementi, ma senza romperli o segmentare ciò che è unito o incollare ciò che è separato.

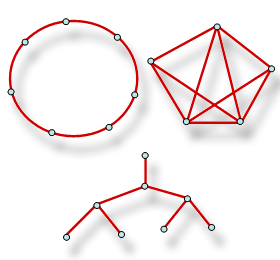
A livello topologico, un triangolo è uguale a un cerchio: uno può essere trasformato nell'altro in modo continuo, senza bisogno di tagliare o incollare. D'altra parte, una circonferenza non può mai essere trasformata in un segmento da un punto di vista topologico, poiché tale trasformazione richiederebbe la rottura della continuità della figura.

Tra le branche della topologia, è possibile distinguere quella generale (detta anche congiuntiva), differenziale e algebrica.

Topologia e reti di comunicazione

Nel campo dell'informatica, la topologia di rete rappresenta un insieme di computer che comunicano tra loro per lo scambio di informazioni, dove ognuno è chiamato nodo. Due possibili "forme" adottate da questo tipo di sistema sono definite come segue:

* stella: ogni nodo è collegato a uno centrale, riducendo il rischio di errori nella rete. In questo modo, affinché i nodi circostanti possano comunicare tra loro, dipendono dall'invio di dati a quello che li collega; quest'ultimo si occupa di trasmetterli agli altri. In caso di comportamento emergente da parte del sistema che invia l'informazione, solo quel pacchetto viene perso, senza influenzare gli altri processi.

Se, invece, il nodo centrale dovesse fallire, il problema sarebbe generale e questo evidenzia l'alto livello di vulnerabilità di questo tipo di progettazione. D'altra parte, il nodo centrale deve eseguire un grande volume di lavoro, che cresce proporzionalmente al numero di nodi collegati ad esso, quindi questa topologia non è adatta nel caso di reti molto grandi.

* albero: basato sul concetto precedente, questa topologia presenta un disegno che collega una serie di reti a stella e le dispone gerarchicamente. In questo modo, ci sono diversi nodi centrali che si dividono le funzioni. Se c'è un problema con una delle "foglie", questa viene isolata; se un'intera sezione fallisce, allora diventa inoperativa, ma non influisce sul resto dell'albero, a differenza di quanto avviene in precedenza.

Grazie a tecniche di indicizzazione e identificazione dei nodi più avanzate di quelle usate in una rete a stella, così come il fatto che è possibile evitare il collasso del sistema aggiungendo più nodi centrali, questa topologia offre più efficienza ed è potenzialmente impossibile da saturare. Tuttavia, l'albero non è giustificato per le piccole strutture, poiché richiede una manutenzione costosa.