Factoring

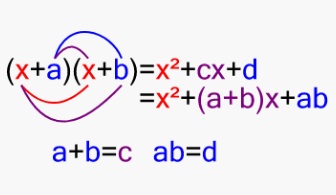
Factoring è un termine usato in matematica per riferirsi all'atto e al risultato della fattorizzazione. Questo verbo (fattorizzare), intanto, si riferisce alla decomposizione di un polinomio nel prodotto di altri polinomi di grado inferiore o all'espressione di un intero dal prodotto delle sue divisioni.

polinomio

Si può dire che la fattorizzazione permette di decomporre un'espressione algebrica in fattori per presentarla in modo più semplice. Va notato che i fattori sono espressioni che subiscono una moltiplicazione per ottenere un prodotto.

Prendiamo il caso della fattorizzazione di numeri interi. Questo processo comporta la decomposizione dei numeri composti in divisori che, moltiplicati, permettono di ottenere il numero in questione.

Secondo il teorema della fattorizzazione unica, noto anche come teorema fondamentale dell'aritmetica, un intero positivo può essere decomposto in un solo modo in numeri primi. Un numero naturale che è maggiore di 1 e ha solo due divisori naturali: 1 e se stesso si chiama numero primo.

Guardiamo il caso del numero 81:

81 / 3
27 / 3
9 / 3
3 / 3
1

La fattorizzazione di 81 in numeri primi, in questo modo, è 3 elevato a 4 (3 x 3 x 3 x 3 x 3 x 3).

Ritornando alla definizione del teorema fondamentale dell'aritmetica, dobbiamo capire che si applica a tutti i numeri interi maggiori di 1, cioè positivi. Sottolinea che in questo gruppo possiamo trovare solo numeri primi o prodotti unici di numeri primi, cioè questa seconda possibilità è fissata per ogni caso. Poiché nel caso della moltiplicazione abbiamo la proprietà commutativa, secondo la quale l'ordine dei fattori non influisce sul prodotto, possiamo alterare la sequenza dei numeri primi risultanti dalla fattorizzazione.

Possiamo anche parlare di fattorizzazione di polinomi. In questo caso, i polinomi sono fattorizzati facendo appello ai coefficienti in un certo campo o dominio. Questi calcoli sono di solito eseguiti con sistemi di algebra per computer. La fattorizzazione delle matrici, infine, si riferisce alla decomposizione di una matrice come prodotto di almeno due matrici.

Guardiamo più da vicino alcuni dei concetti espressi nel paragrafo precedente. Un campo, in questo contesto, è un sistema algebrico in cui le operazioni di addizione e moltiplicazione possono essere eseguite rispettando le proprietà commutative, distributive e associative di queste ultime rispetto alle prime. Ammette anche l'inverso additivo, l'inverso moltiplicativo e due elementi neutri che aprono la porta alla sottrazione e alla divisione (quest'ultima non può essere fatta per zero).

Per quanto riguarda il sistema di algebra del computer, per il quale questo tipo di fattorizzazione rappresenta uno degli strumenti più importanti, si tratta di un programma eseguito da un processore che permette di fare calcoli in modo simbolico. Si differenzia da una calcolatrice tradizionale in quanto permette di risolvere formule ed equazioni in modo simbolico piuttosto che numerico. Questo significa che può interpretare le variabili come tali piuttosto che accettare solo numeri.

La fattorizzazione polinomiale ha una lunga storia. Risale al 1793, quando lo scienziato Hermann Schubert descrisse per la prima volta un algoritmo progettato per questo scopo. Quasi un secolo dopo, nel 1882, Leopold Kronecker continuò a lavorare sulla proposta di Schubert e la espanse per includere polinomi multivariati e a coefficienti.

Nonostante tutto questo, il maggior volume di scoperte e teorie intorno a questo tipo di fattorizzazione emerse nella seconda metà del XX secolo. A grandi linee, possiamo menzionare due gruppi di metodi per calcolare la fattorizzazione polinomiale: quelli classici (ottenere fattori lineari e metodo di Kronecker); quelli moderni (l'algoritmo LLL e il metodo di Trager).