Linee perpendicolari

Una linea è formata, nel contesto della geometria, da una successione indefinita e continua di punti. Secondo la loro posizione o posizione in un piano, le linee possono essere classificate in diversi modi.

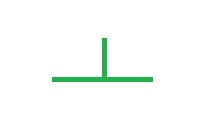
Le linee perpendicolari sono quelle che generano un angolo retto. In altre parole, quando due linee che si intersecano formano un angolo di 90° (un angolo retto), sono perpendicolari.

Su un campo da tennis, per esempio, possiamo trovare diverse linee perpendicolari. Le linee laterali e la linea di fondo sono perpendicolari, così come la linea che separa le caselle di servizio dalla linea di fondo.

In un campo di calcio, intanto, la linea che segna il centro del campo di gioco è perpendicolare alle due linee laterali. Come si può vedere in qualsiasi immagine aerea, l'intersezione della linea di metà campo e ogni linea laterale risulta nella formazione di un angolo di novanta gradi.

È importante notare che nessuna linea è perpendicolare da sola, ma che questa qualificazione dipende dalla relazione specifica che stabilisce con una o più altre linee. Per tornare al caso di un campo di calcio, la linea mediana è perpendicolare alla linea laterale, ma parallela alla linea di base (poiché, per quanto le due linee si estendano in entrambe le direzioni, non si incontreranno mai). Questo dimostra che la stessa linea può essere perpendicolare in una situazione e parallela in un'altra.

Quando due linee si intersecano ma non formano un angolo retto, infine, sono linee oblique. Questo è il caso più comune in natura, poiché ci sono molte, molte più possibilità: mentre per le linee perpendicolari è valido solo un angolo di novanta gradi, per le altre sono validi tutti i valori sotto e sopra questo. Questo non significa che tutti gli esempi che chiamiamo linee perpendicolari siano in realtà linee perpendicolari.

Nella vita quotidiana, quando camminiamo per strada o dentro un edificio, a prima vista possiamo credere che molti oggetti presentino linee perpendicolari, sia nei loro disegni che nelle intersezioni di alcune delle loro parti con quelle di altri oggetti. Dai telai delle porte a un palo della luce conficcato nel terreno, gli esempi sembrano numerosi. In pratica, però, non tutti superano a pieni voti una prova di misura angolare: basta che l'angolo sia leggermente diverso da novanta gradi perché non si possa più chiamare "dritto", e quindi perché le linee che lo formano siano oblique piuttosto che perpendicolari.

Ciò significa che nel discorso quotidiano non è scorretto chiamare due linee perpendicolari se sembrano a occhio nudo formare un angolo di novanta gradi, anche se i numeri non sono esatti. Qualcosa di simile accade con le figure geometriche: parliamo con assoluta facilità di "quadrati", "cerchi" e "triangoli" per descrivere ciò che ci circonda, ma in pratica non ci fermiamo quasi mai a valutare attentamente le forme per sapere se devono davvero essere chiamate così.

Il concetto di linee perpendicolari ha diverse applicazioni, a seconda del campo e della persona. Per esempio, per risolvere il famoso teorema di Pitagora, secondo il quale "la radice quadrata della somma dei quadrati delle gambe di un triangolo è uguale all'ipotenusa", dobbiamo avere i due lati perpendicolari di un triangolo rettangolo, le cosiddette gambe. Per mezzo di questa equazione è possibile eseguire vari compiti che vanno oltre il regno della matematica, come proiettare un punto dell'universo 3D su uno schermo fatto di pixel.