Diedro

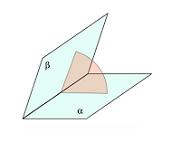
La parola greca díhedros è arrivata in inglese come dihedral, un concetto usato nel campo della geometria. Il termine angolo diedro si riferisce alle porzioni spaziali che sono delimitate da una coppia di semipiani originati sulla stessa linea retta.

Per rappresentare un angolo diedro, è necessario utilizzare due parallelogrammi con un lato comune. Queste figure permettono di simbolizzare i due semipiani che, partendo dallo stesso spigolo, danno origine a questo tipo di angolo.

Ricordiamo che il parallelogramma è definito come un quadrilatero (un poligono con quattro lati e quattro vertici) con la caratteristica che le sue due coppie di lati opposti sono uguali e paralleli. I lati opposti sono definiti come lati che non hanno un vertice comune. L'aspetto del parallelogramma è molto particolare, poiché sembra un quadrato deformato; infatti, i più comuni programmi di editing grafico hanno la possibilità di alterare le immagini in questo modo per ottenere diversi effetti.

L'altro concetto che appare legato al diedro è il bordo, che appartiene anche al campo della geometria. È un segmento di linea il cui scopo è quello di limitare il lato (o la faccia) di una figura piana. Nella branca della geometria conosciuta come geometria dello spazio, che studia le figure di volume che occupano lo spazio, il termine bordo è usato per riferirsi al segmento in cui due facce si incontrano.

Da un piano ausiliario perpendicolare alla linea d'origine si ottiene l'angolo diedro, il cui valore è equivalente all'ampiezza raggiunta dal più piccolo angolo prodotto dalle linee rette appartenenti ai diversi semipiani.

Si può dire, in breve, che un angolo diedro è una regione spaziale formata da due semipiani con una linea in comune. Le facce dell'angolo sono questi semipiani, mentre il suo bordo è la retta comune di cui sopra. La misura, a sua volta, è la più piccola del suo angolo retto.

In base ai suoi angoli, è possibile differenziare tra un diedro concavo e un diedro convesso. I diedri convessi, a loro volta, possono essere ottusi, diritti o acuti. D'altra parte, a seconda delle caratteristiche dei loro angoli rettilinei, si può parlare di diedri supplementari e di diedri complementari.

Viste le limitazioni degli strumenti a disposizione di studenti e insegnanti nelle aule di scuole e facoltà, la rappresentazione degli angoli diedri sulla carta e sulla lavagna di solito non viene fatta con la rilevante deformazione che la prospettiva causerebbe nei semipiani, ma vengono disegnati assonometricamente.