Curva normale

Prima di addentrarci nel significato del termine curva normale, è necessario procedere a scoprire l'origine etimologica delle due parole che la formano:
-Curva è una parola che deriva dal latino, esattamente da "curvus" che può essere tradotto come "curvo".
-Normale, d'altra parte, deriva anch'essa dal latino. Nel suo caso, è il risultato della somma di due componenti perfettamente delimitate: il sostantivo "norma", che è sinonimo di "regola" o "modello", e il suffisso "-al", che si usa per indicare "appartenenza" o "relazione".

Una curva è quella che si allontana continuamente dalla direzione retta, pur senza creare angoli. La linea usata per rappresentare graficamente la grandezza di un fenomeno secondo i valori di una delle sue variabili è anche chiamata curva. Normale, invece, è ciò che è naturale o che funziona come una norma.

Queste idee possono aiutarci a capire cos'è una curva normale, sebbene il concetto abbia un uso specifico nel campo della statistica. Una curva normale è la distribuzione gaussiana: la distribuzione di probabilità di una variabile continua che di solito si avvicina a un fenomeno reale.

L'utilizzo di un modello normale ci permette di assumere che le osservazioni derivino dalla sommatoria di cause indipendenti. La curva normale, in questo quadro, serve a modellare i fenomeni sociali e naturali in un modo che approssima la realtà.

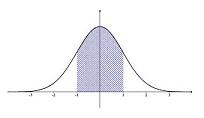
La rappresentazione grafica della curva normale è conosciuta come la campana gaussiana. Questa linea a forma di campana è simmetrica intorno a un certo parametro: c'è una zona centrale concava, che ha il valore medio della funzione al suo centro, e due estremità convesse che tendono ad avvicinarsi all'asse X. La distribuzione gaussiana, quindi, mostra i valori più frequenti al centro della campana, con i valori meno frequenti agli estremi.

Prendiamo il caso dell'altezza media degli uomini tra i 18 e i 60 anni nati in una certa regione. Anche se ci sono persone in quel set che sono alte 1,45 metri e altre che sono alte 2,05 metri, la maggior parte dei soggetti sono alti tra 1,65 e 1,85 metri. La curva normale farà sì che questi valori più comuni si riflettano nel centro della campana gaussiana.

Inoltre, oltre a tutto ciò, non possiamo trascurare il fatto che ci sono altri aspetti rilevanti della curva normale che vale la pena conoscere. Ci riferiamo a quanto segue:
- Permette non solo di "modellare" quelli che sono i fenomeni sociali o naturali ma anche altri fenomeni psicologici.
- L'origine della curva o distribuzione normale si trova nel XVIII secolo. In particolare, è apparso nel 1733 in un articolo scritto dal matematico francese Abraham de Moivre, che è diventato un punto di riferimento in statistica per i contributi che ha dato alla teoria della probabilità. Tuttavia, dopo di lui fu perfezionata da altre figure come Adrien-Maire Legendre e Johann Carl Friedrich Gauss.
- Il suo nome come tale gli fu dato anni dopo. In particolare, gli è stato dato nel 1875 da personaggi come Francis Galton, Charles S. Peirce e Wilhem Lexis.