Correlazione

La correlazione è il legame reciproco o corrispondente che esiste tra due o più elementi. Il concetto è usato in modi diversi a seconda del contesto.

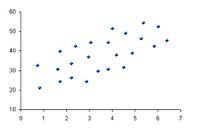
Nel campo della matematica e della statistica, la correlazione si riferisce alla proporzionalità e alla relazione lineare che esiste tra diverse variabili. Se i valori di una variabile cambiano sistematicamente rispetto ai valori di un'altra, si dice che le due variabili sono correlate.

Supponiamo di avere una variabile R e una variabile S. Quando i valori di R aumentano, i valori di S aumentano. Allo stesso modo, quando i valori di S aumentano, i valori di R aumentano. Esiste quindi una correlazione tra le variabili R e S.

Questo stesso esempio può essere presentato graficamente se pensiamo alla contabilità di un'azienda, in particolare a due variabili che registrano "spese per l'acquisto di prodotti" e "stock totale nel magazzino"; è corretto dire che all'aumentare delle prime aumenta anche il secondo, e che non è possibile evitare questa correlazione.

Si può notare che la correlazione è la misura che si registra della dipendenza tra diverse variabili. Il grado di correlazione può essere misurato dai cosiddetti coefficienti di correlazione, come il coefficiente di correlazione intraclasse, il coefficiente di correlazione di Spearman e il coefficiente di Jaspen.

È importante notare che l'esistenza di una correlazione statistica tra due eventi non implica che ci sia una connessione causale tra loro. Tale convinzione fallace è riassunta dall'espressione latina Cum hoc ergo propter hoc, che è spesso riassunta come "la correlazione non implica la causalità". La presunta causalità nella correlazione può essere dovuta alla coincidenza o all'esistenza di qualche fattore sconosciuto, per esempio.

L'idea di correlazione elettronica, d'altra parte, si riferisce all'interazione degli elettroni in un sistema quantistico. Questo concetto cade sotto l'ombrello della meccanica quantistica, una disciplina che la fisica usa per descrivere fondamentalmente la natura su piccole scale spaziali.

La fisica ha preso in prestito questo termine dalla statistica, dove è usato per definire il caso in cui due funzioni di distribuzione non sono indipendenti l'una dall'altra. Per funzione di distribuzione intendiamo una funzione che serve a descrivere la probabilità che la variabile a cui è associata sia minore o uguale a un'altra, intorno alla quale si applica.

Pensiamo, per esempio, a due elettroni, a e b; se dovessimo definire la funzione di distribuzione p(ra,rb) per stabilire la probabilità congiunta che il primo si trovi in ra e il secondo in rb, parleremmo di una correlazione tra di loro nella misura in cui questa non fosse uguale al prodotto di p(ra) per p(rb), cioè delle probabilità individuali di ogni variabile.

La chimica quantistica, invece, è una branca della chimica che può essere applicata alla teoria quantistica dei campi e alla meccanica quantistica; è la descrizione per via matematica del comportamento fondamentale della materia, su una scala misurata in molecole. Nel cosiddetto metodo Hartree-Fock, un'approssimazione delle equazioni della meccanica quantistica per particelle elementari chiamate fermioni, c'è una funzione d'onda asimmetrica che descrive un gruppo di elettroni che è approssimata solo da una tecnica particolare, nota come determinante di Slater.

D'altra parte, le funzioni d'onda esatte non possono sempre essere rappresentate come determinanti singoli, poiché questo lascia fuori la correlazione tra elettroni il cui spin è opposto (lo spin è una proprietà delle particelle elementari che descrive un momento angolare intrinseco il cui valore non cambia).