Ortogonale

Ortogonale è un aggettivo usato per nominare ciò che sta ad un angolo di 90º. È una nozione che, nel caso degli spazi euclidei, è equivalente al concetto di perpendicolarità.

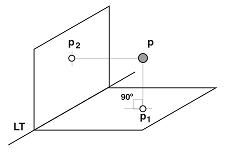
Proiezione ortogonale, d'altra parte, si usa per riferirsi al risultato del disegno di tutte le linee perpendicolari proiettate su un certo piano. Nel fare questa proiezione, si stabilisce un legame tra i punti dell'elemento proiettante e i punti dell'elemento proiettato.

In aggiunta a quanto sopra, possiamo dire che ci sono diversi casi di proiezione ortogonale. Tuttavia, tra le più comuni e significative ci sono le due seguenti:
- La proiezione ortogonale di un segmento.
- La proiezione ortogonale di un punto.

Non è meno importante sottolineare che, come regola generale, quando si parla di proiezione o base ortogonale, lo si fa nel campo della geometria euclidea. Questa, chiamata anche parabolica o euclidea, è quel ramo di studio o disciplina che si occupa di analizzare le proprietà degli spazi geometrici in cui sono soddisfatti gli assiomi di Euclide. Cioè, nello spazio tridimensionale, nella linea retta reale o nel piano euclideo.

Il geometra e matematico Euclide (325 - 265 a.C.) è la personalità che ha plasmato questa disciplina, che si basa su diversi pilastri come il libro che ha scritto con il titolo "Gli elementi". Tuttavia, altri contributi sono stati dati in seguito da figure come Felix Klein, attraverso il suo "Programma di Erlangen".

Supponiamo di voler fare la proiezione ortogonale di un segmento PR su una retta T. Per questo dovremo proiettare le estremità di PR attraverso linee che sono perpendicolari a T, il che ci permetterà di conoscere la proiezione ortogonale del segmento su questa retta. L'intersezione tra le linee di proiezione e T crea un nuovo segmento, che potremmo chiamare MN. Quando il segmento PR è parallelo alla linea T, il segmento MN sarà analogo a PR.

Si può dire che la disposizione ortogonale è basata su un angolo retto, sviluppandosi nello spazio orizzontale e nello spazio verticale. Questa idea non si applica solo nel campo della geometria, ma è importante anche nell'arte. Gli artisti devono imparare a lavorare con l'ortogonalità in senso estetico per rendere l'aspetto visivo di un dipinto attraente.

C'è spesso confusione tra ciò che è noto come base ortogonale e la base ortonormale. Tuttavia, sono diversi e bisogna sapere quali:
- Il primo è uno spazio se i vettori che lo formano hanno la particolarità di essere perpendicolari a due a due.
- Il secondo, invece, è quello che ha uno spazio dato la cui base è ortogonale e anche i suoi vettori hanno la caratteristica di essere unitari.

I cerchi possono anche essere ortogonali quando sono secanti e, in un dato punto, le loro rispettive tangenti sono perpendicolari. Rispetto a un punto di intersezione, i loro raggi saranno anche perpendicolari.