Varianza

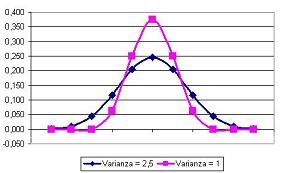
La nozione di varianza è spesso usata nel campo della statistica. È una parola inventata dal matematico e scienziato inglese Ronald Fisher (1890-1962) ed è usata per identificare la media delle deviazioni quadratiche di una variabile casuale, considerando il valore medio della variabile.

La varianza delle variabili casuali, quindi, è una misura relativa alla loro dispersione. È l'aspettativa del quadrato della deviazione della variabile in esame dalla sua media e si misura in un'unità diversa. Per esempio: nei casi in cui la variabile misura una distanza in chilometri, la sua varianza è espressa in chilometri al quadrato.

Si noti che le misure di dispersione (identificate anche con il nome di misure di variabilità) si occupano di esprimere la variabilità di una distribuzione mediante un numero, nei casi in cui i diversi punteggi della variabile sono molto lontani dalla media. Più alto è il valore della misura di dispersione, maggiore è la variabilità. Più basso è il valore, maggiore è l'omogeneità.

Quello che fa la varianza è stabilire la variabilità della variabile casuale. È importante tenere a mente che, in certi casi, è preferibile usare altre misure di dispersione date le caratteristiche delle distribuzioni.

La varianza di campionamento è quando la varianza di una comunità, gruppo o popolazione è calcolata sulla base di un campione. La covarianza, d'altra parte, è la misura della dispersione congiunta di una coppia di variabili.

Gli esperti parlano di analisi della varianza per indicare l'insieme dei modelli statistici e le loro procedure associate in cui la varianza è partizionata in componenti distinte.

La deviazione standard

Uno dei concetti più importanti legati alla varianza è la deviazione standard, nota anche come deviazione standard, che rappresenta la grandezza della dispersione delle variabili di intervallo e di rapporto, ed è molto utile nel campo della statistica descrittiva. Per ottenerla, si parte semplicemente dalla varianza e si calcola la sua radice quadrata.

In pratica, se abbiamo i valori (espressi in millimetri) 14mm, 11mm, 10mm, 6mm e 4mm, possiamo calcolare la loro media sommandoli e dividendo il risultato per 5, che è il numero di elementi. Avremmo la 9mm. Per conoscere la varianza, dobbiamo sottrarre ognuno dei valori dalla media appena mostrata, elevare al quadrato ogni risultato (per evitare che i numeri negativi influenzino lo studio), sommarli e, infine, dividere tutto per 5. La varianza è di 93,8 millimetri quadrati. Infine, per trovare la deviazione standard, calcoliamo la radice quadrata, che ci lascia 9,68mm (si noti che l'unità è di nuovo millimetri).

Questi dati sono molto utili e necessari per analizzare e descrivere le informazioni, poiché offrono diversi punti di vista, così come diverse tendenze nei dati che caratterizzano l'oggetto in questione e ci permettono di stabilire parametri di confronto più complessi e dinamici che semplici valori isolati o semplicemente sottoposti alla loro media aritmetica.

Nel processo di verifica di una teoria, è importante anticipare i possibili risultati, e la deviazione serve ad analizzare il comportamento dei valori intorno alla loro media. Stabilisce nuovi punti che aprono le porte a classificazioni diverse e a dati che potrebbero non essere stati considerati in primo luogo.

Utilizzando solo la media tra un insieme di valori, non è possibile sapere se qualcuno di essi è eccessivamente lontano dalla "normalità" esistente in quel contesto. La deviazione standard permette di stabilire due nuovi limiti intorno a questa linea centrale, per sapere quando un elemento è troppo piccolo o troppo grande.