Parallelepipedo

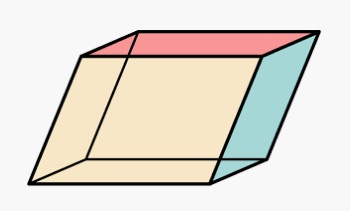
La parola greca parallēlepipedon deriva dal tardo latino parallelepipĕdum, che è l'antecedente etimologico più vicino del parallelepipedo: un corpo geometrico delimitato da sei parallelogrammi e avente le facce opposte parallele ed uguali.

Si noti che, in geometria, un corpo o solido è un oggetto che ha le tre dimensioni più importanti (altezza, larghezza e lunghezza). Nel caso specifico del parallelepipedo, è un poliedro: un corpo formato da superfici piane.

I parallelepipedi, in breve, sono esaedri (poliedri che hanno sei facce). Tutte le loro facce sono parallelogrammi (quadrilateri con i lati opposti paralleli e uguali); tra i parallelogrammi del parallelepipedo, quelli opposti sono identici e paralleli.

Ogni parallelepipedo ha otto vertici e dodici bordi. Poiché i vertici sono disposti in una coppia di piani paralleli, il parallelepipedo è un prismatoide. I bordi, invece, sono paralleli e uguali a gruppi di quattro.

In base alle loro caratteristiche, è possibile differenziare diversi tipi particolari di parallelepipedi. Il parallelepipedo i cui parallelogrammi sono quadrati si chiama cubo o esaedro regolare. Il parallelepipedo formato da rombi, invece, è un parallelepipedo obliquo o romboedro, mentre il parallelepipedo formato da rettangoli è un parallelepipedo rettangolare o ortoedro. Se tutte e sei le facce del parallelepipedo sono romboidi, è un romboedro.

I parallelepipedi si possono trovare in molte situazioni quotidiane. Un mattone, per esempio, è un parallelepipedo: di solito ha quattro rettangoli (due opposti tra loro) e due quadrati (anch'essi opposti tra loro).

I calcoli delle sue proprietà sono relativamente più complessi di quelli di una figura bidimensionale, poiché il parallelepipedo ne ha tre; tuttavia, come di solito accade in questi casi, si basano sulle formule dell'universo bidimensionale come punto di partenza. Prendiamo per esempio il volume, cioè la grandezza definita come l'estensione tridimensionale di una regione: per calcolarlo, prima di tutto, bisogna trovare l'area di una delle sue facce (può essere una qualsiasi) e poi moltiplicarla per l'altezza della figura che parte da essa.

La formula che risponde a questo calcolo si esprime come segue: V = A h, dove V è il volume, A è l'area e h è l'altezza. Questo è usato nella maggior parte dei casi, ma ce n'è uno che semplifica notevolmente il calcolo: quello in cui tutte le facce del parallelepipedo sono perpendicolari tra loro. Per fare questo, è sufficiente moltiplicare la sua altezza, larghezza e lunghezza, partendo da uno qualsiasi dei suoi vertici e misurando i tre bordi che convergono su di esso.

Queste lunghezze sono rappresentate da tre lettere, che danno il nome ai bordi, e la formula risultante è la seguente: V = w u v. Naturalmente, c'è un caso ancora più semplice, sebbene sia più legato al precedente che al primo: il cubo. Non dimentichiamo che questa figura ha tutti i suoi bordi di lunghezza uguale, così come il quadrato ha quattro lati identici. In questo caso, basta al cubo questa estensione: V = l3.

D'altra parte, possiamo affermare che se capiamo che i tre spigoli che si incontrano in uno stesso vertice sono tre vettori, allora per calcolare il suo volume possiamo trovare il prodotto misto e quindi il suo valore assoluto: V = |a . (b x c)|. Questo ci mostra che il modo di studiare la stessa figura geometrica dipende dalle sue caratteristiche particolari, ma anche dalle necessità, conoscenze e preferenze della persona. Quando si traduce in un computer, la scelta di un metodo o di un altro dipende a volte da quanto è impegnativo per il processore.