Coseno

L'idea di coseno è usata nel campo della geometria. Il coseno, in questo contesto, è il seno del complemento di un arco o di un angolo, dice la Reale Accademia Spagnola (RAE) nel suo dizionario. L'abbreviazione ufficiale di questa funzione trigonometrica è cos, ed è così che la troviamo nelle equazioni e nelle calcolatrici.

Si noti che il seno è il risultato della divisione tra la gamba opposta di un angolo e l'ipotenusa (in un triangolo rettangolo, il lato maggiore è l'ipotenusa, mentre gli altri due - che formano l'angolo di 90º - sono chiamati gambe). Il complemento, invece, è l'angolo che, aggiunto a un altro, completa un angolo di 90°.

Questi concetti appartengono al ramo della matematica noto come trigonometria, che si concentra sull'analisi dei cosiddetti rapporti trigonometrici, tra i quali ci sono i seguenti quattro, oltre a seno e coseno: tangente, secante, cotangente e cosecante.

Nella scuola secondaria, la trigonometria è di solito inclusa nell'ultima fase del programma, poiché è una parte molto complessa e difficile da capire per coloro che non hanno un legittimo gusto per i numeri. Il suo intervento nelle altre branche della matematica è a volte diretto, a volte indiretto; a grandi linee, possiamo dire che la sua applicazione avviene ogni volta che si rende necessario fare misure con un alto grado di precisione.

Supponiamo di avere un triangolo rettangolo ABC, con un angolo di 90º e due angoli di 45º. Dividendo una delle gambe opposte a un angolo di 45º e l'ipotenusa, otteniamo il seno e poi possiamo calcolare il coseno.

Un altro modo più semplice per calcolare il coseno in un triangolo rettangolo è dividere la gamba adiacente a un angolo acuto e l'ipotenusa. Il seno si ottiene dividendo la gamba opposta e l'ipotenusa, mentre la tangente comporta la divisione della gamba opposta e della gamba adiacente. Queste tre funzioni (coseno, seno e tangente) sono le più importanti in trigonometria.

Se un triangolo ha un'ipotenusa di 4 centimetri, un cateto opposto di 2 centimetri e un cateto adiacente di 3,4 centimetri, il suo coseno sarà 0,85:

Coseno = Cateto adiacente / ipotenusa
Coseno = 3,4 / 4
Coseno = 0,85

La funzione secante, invece, consiste nel dividere 1 per il coseno. Nell'esempio sopra, la secante è 1,17.

La legge dei coseni, conosciuta anche come teorema del coseno, è una generalizzazione del noto teorema di Pitagora. È la relazione che si può stabilire tra uno dei lati di un triangolo rettangolo con gli altri due lati e il coseno dell'angolo che formano.

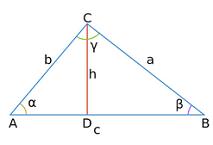
In un triangolo ABC, con angoli α, β, γ e lati a, b, c (opposti ai precedenti, nel rispettivo ordine), il teorema del coseno può essere definito come mostrato nell'immagine: c al quadrato è uguale alla somma di a al quadrato e b al quadrato, meno il doppio del prodotto ab cosγ.

Un altro modo di definire il coseno è quello di intenderlo come:

* una funzione pari: in matematica, questa classificazione viene data alle funzioni di variabili reali tenendo conto della loro parità. Ci sono tre possibilità: possono essere pari, dispari o non avere parità;

* una funzione continua: è una funzione matematica in cui i punti vicini al dominio portano una serie di piccole variazioni nei loro valori;

* una funzione trascendente: è una funzione che non può soddisfare un'equazione polinomiale con coefficienti che sono polinomi (un polinomio è un'espressione composta da una somma di prodotti di costanti e variabili tra loro).