Punti collineari

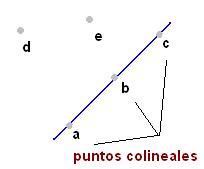
La nozione di punti collineari appare in geometria per riferirsi a punti che giacciono sulla stessa linea retta. Per comprendere precisamente il concetto, quindi, dobbiamo sapere cos'è un punto in geometria e cos'è una linea.

Entrambi (punti e linee), insieme ai piani, formano l'insieme di quelli che sono conosciuti come gli enti fondamentali della geometria. Sono elementi che si definiscono in base al legame che stabiliscono con altri simili.

Il punto non è un elemento fisico, ma una figura priva di superficie, volume e lunghezza: cioè, non ha dimensioni, ma si usa per nominare una posizione specifica all'interno di uno spazio.

L'idea di linea o retta, invece, si riferisce a una successione infinita di punti che si estende nella stessa direzione e in una sola dimensione. Le linee non hanno né inizio né fine.

Con tutto questo in mente, è facile capire cosa sono i punti collineari. I punti che possono essere uniti dalla stessa linea retta sono collineari. In altre parole: i punti collineari sono quelli che sono uniti da una linea retta (la linea retta passa attraverso tutti loro). Quel punto che si trova al di fuori della linea in questione non è collineare al resto.

Dati tre punti, vediamo ora come verificare se sono collineari per mezzo di una formula. In primo luogo, è consigliabile tracciare i punti su un piano e definire i segmenti di linea che possono essere visti tra ogni coppia. Avendo questi valori, possiamo quindi procedere a mettere due dei punti nella formula per la distanza tra due punti, che assomiglia molto a quella usata per calcolare la lunghezza dell'ipotenusa, secondo il Teorema di Pitagora: la distanza è uguale alla radice quadrata della somma dei quadrati di (x2 - x1) e (y2 - y1), come mostrato nell'immagine a destra.

Le variabili x1 e y1 corrispondono alle coordinate bidimensionali del primo punto scelto, mentre x2 e y2 sono quelle del secondo. Per controllare se abbiamo davanti a noi tre punti collineari, dobbiamo calcolare la distanza tra ogni punto estremo e quello intermedio, e verificare se la somma dei due valori è uguale alla distanza tra i punti estremi.

Anche se può sembrare inutile usare la formula una volta che abbiamo fatto il grafico, è importante notare due cose: quando i valori hanno dei decimali o quando la distanza tra loro è considerevole, non è facile dare un verdetto semplicemente guardandoli sul piano; le persone più esperte saltano questo passo e usano direttamente l'equazione, poiché fa risparmiare tempo e diminuisce le possibilità di errore.

Per quanto riguarda le applicazioni di questo concetto, uno dei settori più vicini al grande pubblico che combina l'uso della matematica e della grafica è l'industria dei videogiochi, e lo fa anche se non sempre viene notato dai giocatori. In titoli dall'aspetto semplice come i minigiochi di tiro al bersaglio, per esempio, che usano una fionda (conosciuta anche come fionda o slingshot) come arma, il processore deve calcolare costantemente la posizione di vari punti per, secondo il codice scritto dagli sviluppatori, dare una risposta sullo schermo.

Nel caso della fionda, una delle tante tecniche per sapere se il giocatore sta mirando correttamente può consistere nel controllare se la posizione della mano virtuale, quella del punto medio della forcella e quella del bersaglio sono collineari.